Công thức lượng giác 11
Công thức cộng
sin(a ± b)=sin a cos b ± cos a sin b
cos(a ± b)=cos a cos b ∓ sin a sin b
tan(a ± b)=(tan a ± tan b) / (1 ∓ tan a tan b) (điều kiện: tan a * tan b ≠ 1)
Công thức nhân đôi
sin 2a=2 sin a cos a
cos 2a=cos² a – sin² a=2cos² a – 1=1 – 2sin² a
tan 2a=(2 tan a) / (1 – tan² a) (điều kiện: tan a ≠ ± 1)
Công thức nhân ba
sin 3a=3 sin a – 4 sin³ a
cos 3a=4 cos³ a – 3 cos a
tan 3a=(3 tan a – tan³ a) / (1 – 3 tan² a)

Công thức lượng giác gồm những nội dung chính nàoCông thức hạ bậc
sin² a=(1 – cos 2a) / 2
cos² a=(1 + cos 2a) / 2
sin² a cos² a=(1 – cos 4a) / 8
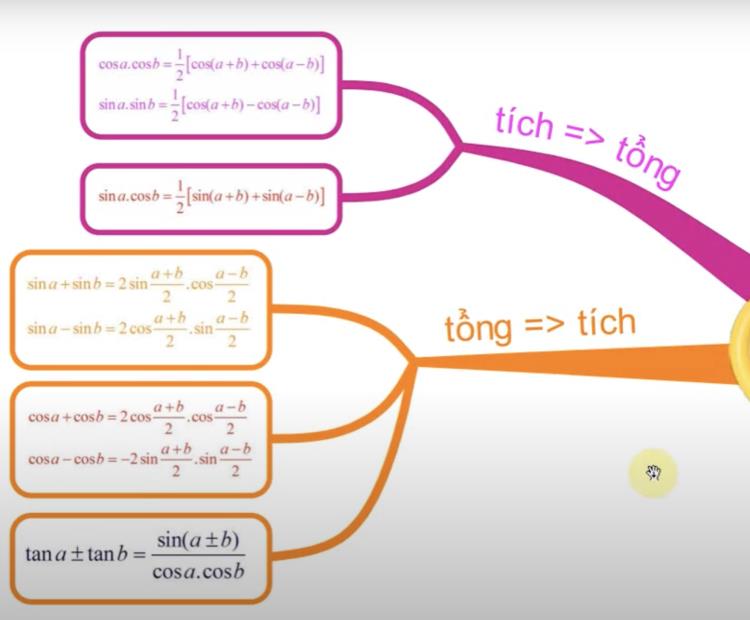
Công thức tích thành tổng
sin a sin b=1/2 [cos(a – b) – cos(a + b)]
cos a cos b=1/2 [cos(a – b)+cos(a + b)]
sin a cos b=1/2 [sin(a + b)+sin(a – b)]
Công thức tổng thành tích
sin a+sin b=2 sin((a + b)/2) cos((a – b)/2)
sin a – sin b=2 cos((a + b)/2) sin((a – b)/2)
cos a+cos b=2 cos((a + b)/2) cos((a – b)/2)
cos a – cos b=– 2 sin((a + b)/2) sin((a – b)/2)
Để học nhanh và nhớ lâu công thức lượng giác lớp 11, bạn có thể áp dụng một số cách sau:
Hiểu bản chất thay vì học vẹt
Nhớ công thức cộng → từ đó suy ra công thức nhân đôi, hạ bậc.
Ví dụ: sin² a=(1 – cos2a)/2 được rút ra từ cos2a=1 – 2sin² a.
Làm thế nào để học nhanh và nhớ lâu công thức lượng giácNhóm công thức theo từng “ cụm”
Cộng – trừ: sin(a ± b), cos(a ± b), tan(a ± b).
Nhân đôi – nhân ba.
Hạ bậc – biến đổi tích thành tổng.
👉 Việc học theo nhóm giúp não dễ hệ thống và nhớ lâu hơn.
Sử dụng sơ đồ tư duy hoặc bảng tổng hợp
Viết lại công thức trên 1 tờ giấy A4 hoặc mindmap.
Dán trước bàn học, ôn lại hằng ngày.
Dễ nhớ hơn nhiều so với đọc rời rạc trong sách.
Luyện bài tập biến đổi thường xuyên
Áp dụng công thức vào bài tập biến đổi lượng giác.
Càng làm nhiều, não càng “ quen tay” và nhớ công thức tự nhiên.
Dùng mẹo ghi nhớ nhanh
Công thức cộng: “ Sin thì cùng dấu, Cos thì đổi dấu.”
Công thức hạ bậc: luôn có dạng (1 ± cos2a)/2.
Công thức tích – tổng: nhớ từ khóa “ tích → cos, tổng → sin.”
Ôn tập bằng flashcard hoặc app học nhanh
Ghi công thức 1 mặt, kết quả mặt kia.
Dùng app Quizlet, Anki để tự kiểm tra.
👉 Tóm lại: Hiểu bản chất+học theo nhóm+luyện bài tập+dùng mẹo nhớ nhanh=nhớcông thức lượng giác lâu dài, không sợ quên khi thi.
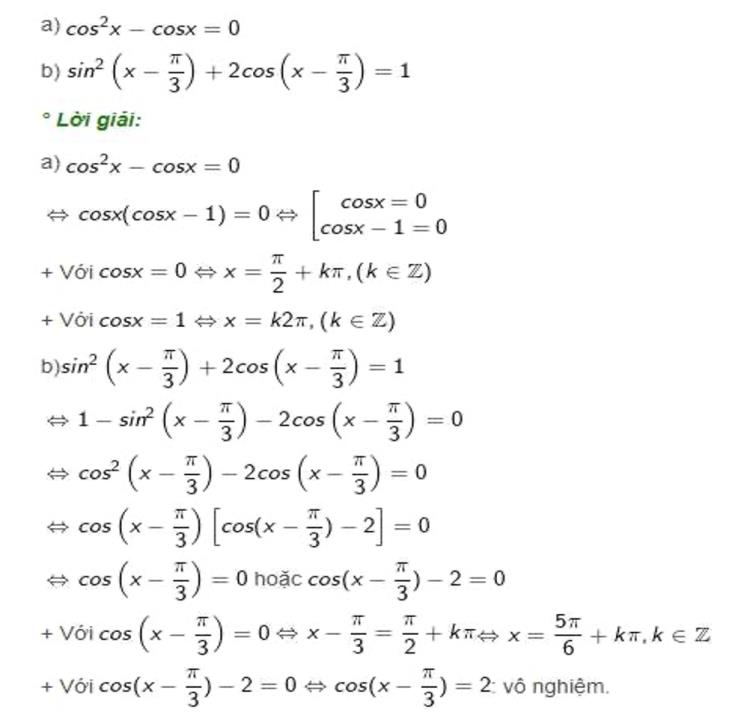
Bài tập áp dụng công thức lượng giác thường gặp trong đề thiCông thức lượng giác lớp 11 có vai trò rất quan trọng trong việc giải toán, bởi chúng xuất hiện ở hầu hết các dạng bài từ đại số đến hình học. Khi nắm vững và biết cách vận dụng, học sinh có thể biến những bài toán tưởng chừng phức tạp trở nên ngắn gọn và dễ xử lý hơn.
- Biến đổi và rút gọn biểu thức lượng giác: Các công thức lượng giác giúp đưa biểu thức phức tạp về dạng đơn giản, dễ quan sát mối quan hệ giữa các hàm sin, cos, tan. Ví dụ, cos2x có thể thay bằng 1 – 2sin² x hoặc 2cos² x – 1 để thuận lợi cho việc biến đổi và rút gọn biểu thức.
- Giải phương trình và bất phương trình lượng giác: Nhờ công thức nhân đôi, hạ bậc, nhiều phương trình phức tạp có thể đưa về dạng cơ bản như sin x=a, cos x=b, tan x=c. Điều này giúp giải nhanh và chính xác, đồng thời hỗ trợ trong việc giải bất phương trình lượng giác.
- Ứng dụng trong hình học phẳng: Công thức lượng giác là công cụ quan trọng để chứng minh các đẳng thức hình học và giải tam giác. Các định lý như sinA/a=sinB/b=sinC/c hay định lý cos giúp tính cạnh, góc hoặc diện tích tam giác (S=1/2 ab sinC).
- Ứng dụng trong vật lý và thực tế: Công thức lượng giác không chỉ dùng trong toán học mà còn xuất hiện trong các hiện tượng vật lý: dao động điều hòa, sóng cơ, sóng âm, giao thoa ánh sáng, dòng điện xoay chiều… Nhờ đó, học sinh có thể thấy rõ mối liên hệ giữa toán học và thế giới thực.
Tóm lại, công thức lượng giác lớp 11 là chìa khóa để biến đổi biểu thức, giải phương trình, chứng minh đẳng thức, giải tam giác và ứng dụng trong các bài toán thực tế. Việc nắm chắc và luyện tập thường xuyên sẽ giúp học sinh thành thạo và tự tin khi gặp các dạng bài toán đa dạng.
Dưới đây là một số bài tập điển hình áp dụng công thức lượng giác lớp 11 thường gặp trong đề thi, kèm theo lời giải chi tiết và dễ hiểu:
Bài tập 1: Biến đổi biểu thức lượng giác
Bài toán:
Rút gọn biểu thức:
sin x * cos x
Lời giải:
Sử dụng công thức nhân đôi:
sin 2x=2 sin x cos x → sin x cos x=1/2 sin 2x
Kết quả:
sin x * cos x=1/2 sin 2x
Bài tập 2: Giải phương trình lượng giác
Bài toán:
Giải phương trình:
2 sin² x – 3 sin x+1=0
Lời giải:
Đặt y=sin x, phương trình trở thành:
2y² – 3y+1=0
Giải phương trình bậc hai:
y=(3 ± √ (9 – 8)) / 4=(3 ± 1)/4 → y=1 hoặc y=1/2
Vậy:
sin x=1 → x=π/2+2kπ
sin x=1/2 → x=π/6+2kπ hoặc x=5π/6+2kπ
Bài tập 3: Biến đổi tổng thành tích
Bài toán:
Rút gọn biểu thức:
sin 75° +sin 15°
Lời giải:
Sử dụng công thức tổng thành tích:
sin a+sin b=2 sin((a+b)/2) * cos((a-b)/2)
Áp dụng:
sin 75° +sin 15° =2 sin((75° +15° )/2) * cos((75° – 15° )/2)
=2 sin 45° * cos 30°
=2 * 0.7071 * 0.8660 ≈ 1.2247
Kết quả:
sin 75° +sin 15° ≈ 1.225
Bài tập 4: Giải tam giác áp dụng định lý sin
Bài toán:
Cho tam giác ABC, biết a=6, B=45° , C=60° . Tính cạnh b.
Lời giải:
Tính góc A: A=180° – B – C=75°
Áp dụng định lý sin:
a / sin A=b / sin B → b=a * sin B / sin A
b=6 * sin 45°/ sin 75° ≈ 6 * 0.7071 / 0.9659 ≈ 4.39
Kết quả:
b ≈ 4.39
Trên đây chúng tôi đã tổng hợp đầy đủ các kiến thức và bài tập áp dụng về Công thức lượng giác, bao gồm công thức cộng, nhân đôi, hạ bậc, biến đổi tổng – tích và cách giải phương trình, chứng minh đẳng thức. Hy vọng bài viết sẽ giúp các em học sinh nắm vững kiến thức, vận dụng thành thạo vào học tập và các kỳ thi sắp tới.>> Xem thêm: Taxi nội bài thái nguyên