[MỤC LỤC] 1.Nhị thức Newton là gì? 2.Công thức tính nhị thức Newton như thế nào 3.Cách giải bài tập áp dụng nhị thức Newton hiệu quả? 4.Các dạng bài tập thường gặp về nhị thức Newton? 5.Nhị thức Niu tơn có ứng dụng gì trong Toán học và thực tế? |
Nhị thức newton
Nhị thức Niu tơn là một định lý trong toán học dùng để khai triển lũy thừa của một tổng hai số hạng. Định lý này cho phép biểu diễn (a + b)ⁿ thành một đa thức gồm nhiều số hạng, trong đó hệ số của từng số hạng được xác định theo quy luật tổ hợp.
Công thức khai triển nhị thức Niu tơn được viết như sau:
(a + b)ⁿ=Σ (k=0 → n) C(n, k) · aⁿ⁻ᵏ · bᵏ
Trong đó:
Σ (k=0 → n): tổng các hạng tử từ k=0 đến k=n
C(n, k): số tổ hợp chập k của n, tính bằng công thức n ! / (k !(n− k) !)
aⁿ⁻ᵏ, bᵏ: lũy thừa tương ứng của a và b
👉 Đây là công thức tổng quát, dùng để khai triển biểu thức (a + b)ⁿ thành một đa thức.
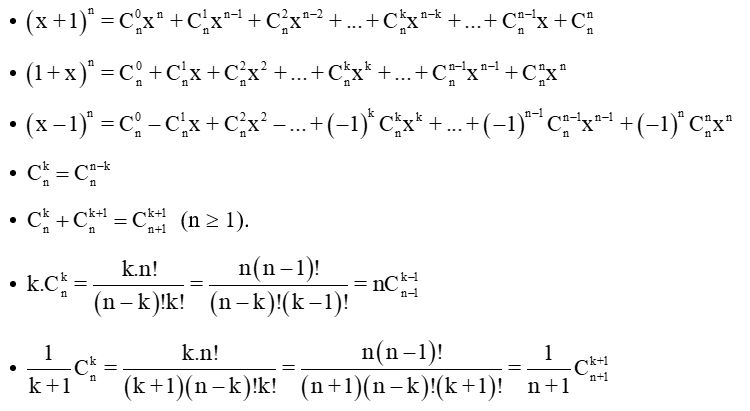
Công thức tính nhị thức Niu tơn như thế nàoDưới đây là phương pháp và mẹo hiệu quả để giải nhanh các bài tập áp dụng nhị thức Niu tơn.
Checklist giải bài nhanh
Nhận diện dạng: có phải dạng (a + b)ⁿ hay biến đổi thành dạng đó không?
Xác định mục tiêu: khai triển toàn bộ, tìm hệ số của xᵏ, tìm hằng số, tổng các hệ số, tổng chẵn/lẻ, hay tổng có trọng số?
Chọn công cụ phù hợp: trực tiếp khai triển (n nhỏ), dùng hệ số C(n, k), sử dụng biến thế (x=1, x=− 1), đạo hàm/vi phân để lấy tổng có trọng số, hoặc nhận xét đối xứng.
Áp công thức:
(a + b)ⁿ=Σ (k=0 → n) C(n, k) · aⁿ⁻ᵏ · bᵏ
Kiểm tra tính đối xứng: hệ số C(n, k)=C(n, n− k) giúp rút gọn.
Nếu bài có hệ số nhân béo (như (2x − 3)⁸), phân tách thành aⁿ⁻ᵏ· bᵏ và tính số mũ/tiên tố trước khi rút gọn.
Mẹo & kỹ thuật hay dùng
Tìm tổng các hệ số: đặt a=1, b=1 → (1 + 1)ⁿ=2ⁿ.
Tổng hiệu (chẵn − lẻ): đặt a=1, b=− 1 → (1 − 1)ⁿ=0 (dùng để tách tổng chẵn/lẻ).
Hằng số (không chứa x): trong (x + c)ⁿ, hằng số là cⁿ (tương tự khi có hệ số trước x, cần chỉnh).
Tìm hệ số của xᵏ trong (ax + b)ⁿ: hệ số=C(n, k) · aᵏ · bⁿ⁻ᵏ (lưu ý vị trí k tương ứng).
Dùng đối xứng: hệ số của xᵏ và xⁿ⁻ᵏ liên quan qua C(n, k)=C(n, n− k).
Dùng đạo hàm: ví dụ tổng k· C(n, k) có thể lấy bằng n· 2ⁿ⁻¹ (do đạo hàm của (1+x)ⁿ tại x=1).
Rút gọn nhanh bằng tam giác Pascal khi n nhỏ (n ≤ 6– 7).
Các dạng bài thường gặp & hướng xử lý
Khai triển toàn phần (n nhỏ): nhân trực tiếp theo công thức.
Tìm hệ số của xᵏ: dùng công thức hệ số (như trên).
Tìm số hạng chứa xᵏ: tìm k thỏa điều kiện số mũ.
Tổng các hệ số, tổng chẵn/lẻ: dùng x=1 hoặc x=− 1.
Tổng có trọng số (k· C(n, k), k² · C(n, k)): dùng đạo hàm của (1 + x)ⁿ rồi đặt x=1.
Hằng số trong biểu thức phức tạp: tách các nhân tử, tìm tổ hợp sao cho lũy thừa x bằng 0.
Bài chứng minh đẳng thức tổ hợp: suy từ khai triển và so sánh hệ số.
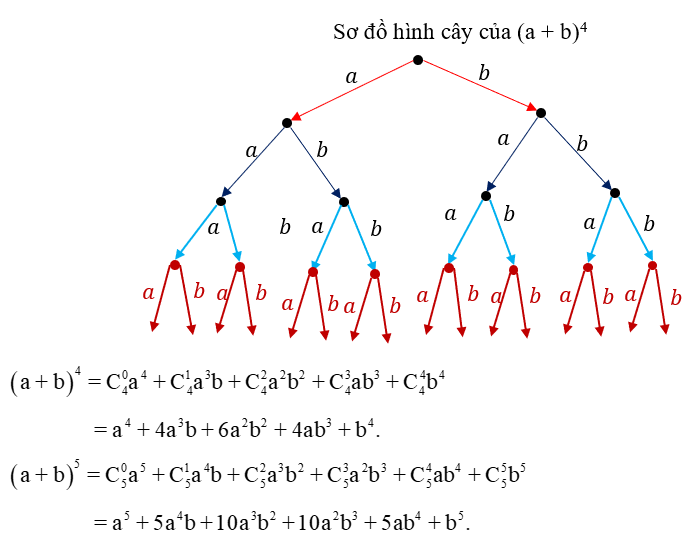
Cách giải bài tập áp dụng nhị thức Niu tơn hiệu quả?Dưới đây là tổng hợp các dạng bài tập thường gặp về nhị thức Niu tơn, kèm theo cách tiếp cận ngắn gọn:
🔹 1. Khai triển biểu thức
Dạng: Khai triển (a + b)ⁿ thành đa thức.
Cách làm: Dùng công thức tổng quát hoặc tam giác Pascal (n nhỏ).
🔹 2. Xác định số hạng tổng quát
Dạng: Tìm công thức số hạng thứ k trong khai triển (ax + b)ⁿ.
Cách làm: Sử dụng công thức:
T₍ₖ₊₁₎=C(n, k) · (ax)ᵏ · bⁿ⁻ᵏ
🔹 3. Tìm hệ số của xᵐ
Dạng: Xác định hệ số đứng trước xᵐ trong (ax + b)ⁿ.
Cách làm: Giải điều kiện số mũ của x=m, sau đó tính hệ số bằng công thức.
🔹 4. Tìm số hạng chứa xᵐ
Dạng: Trong khai triển (ax + b)ⁿ, tìm số hạng chứa xᵐ.
Cách làm: Tìm k sao cho mũ của x bằng m.
🔹 5. Tìm tổng các hệ số
Dạng: Tính tổng hệ số trong khai triển (ax + b)ⁿ.
Cách làm: Thay x=1 → (a + b)ⁿ.
🔹 6. Tổng hệ số theo điều kiện chẵn/lẻ
Dạng: Tính tổng các hệ số hạng chẵn hoặc lẻ.
Cách làm:
Tổng tất cả: (1 + 1)ⁿ=2ⁿ
Hiệu chẵn – lẻ: (1 − 1)ⁿ=0
⇒ Tách được tổng chẵn hoặc tổng lẻ.
🔹 7. Tìm hệ số/hạng không chứa biến
Dạng: Trong khai triển (axᵖ + bq)ⁿ, tìm hạng không chứa x.
Cách làm: Giải điều kiện số mũ của x bằng 0.
🔹 8. Các bài toán tổng quát với tổ hợp
Dạng: Chứng minh các đẳng thức tổ hợp bằng nhị thức Niu tơn.
Ví dụ: Σ C(n, k)=2ⁿ; Σ k· C(n, k)=n· 2ⁿ⁻¹ .
👉 Đây là 8 dạng phổ biến nhất, thường xuất hiện trong đề thi THPT.
Các dạng bài tập thường gặp về nhị thức Niu tơn🔹 1. Trong Toán học
Khai triển nhanh đa thức: Giúp khai triển (a + b)ⁿ mà không cần nhân lặp lại nhiều lần.
Tổ hợp và xác suất: Hệ số nhị thức C(n, k) liên quan trực tiếp đến số cách chọn k phần tử từ n, dùng nhiều trong xác suất thống kê.
Chứng minh đẳng thức tổ hợp: Nhị thức Niu tơn thường dùng để chứng minh và suy ra các công thức như Σ C(n, k)=2ⁿ, Σ k· C(n, k)=n· 2ⁿ⁻¹ , ...
Tính giới hạn và gần đúng: Dùng khai triển để xấp xỉ giá trị biểu thức, ví dụ (1 + x)ⁿ khi x nhỏ.
Giải tích và chuỗi số: Liên hệ với khai triển Taylor, khai triển nhị thức với số mũ thực (hoặc phức).
🔹 2. Trong thực tế
Thống kê và xác suất thực tiễn: Dự đoán kết quả trong trò chơi, mô phỏng rủi ro trong tài chính, tính xác suất trong di truyền học (thừa hưởng gen).
Tin học và mật mã: Dùng tổ hợp nhị thức trong thuật toán, mã hóa, lý thuyết đồ thị.
Vật lý: Khai triển nhị thức để xấp xỉ công thức, ví dụ tính gần đúng lực hấp dẫn, chuyển động dao động nhỏ.
Kinh tế học: Ước lượng lãi suất kép, mô hình tăng trưởng, tính toán xác suất rủi ro.
Khoa học dữ liệu: Áp dụng trong mô hình nhị phân, phân phối nhị thức (binomial distribution).
Có thể thấy, nhị thức Niu tơn không chỉ là một định lý quan trọng trong chương trình toán học mà còn là công cụ hữu ích trong tổ hợp, xác suất và nhiều lĩnh vực khác. Việc nắm vững định lý này sẽ giúp bạn học tốt hơn và áp dụng linh hoạt trong thực tế.