Tính chất hình bình hành
Trong hình học phẳng, hình bình hành là một tứ giác có các cạnh đối song song từng đôi một. Điều này có nghĩa là hai cạnh đối diện không chỉ song song mà còn bằng nhau về độ dài. Hình bình hành là một trường hợp đặc biệt trong tập hợp các tứ giác lồi, có nhiều tính chất và ứng dụng quan trọng trong toán học, đặc biệt là trong các bài toán hình học và hình học tọa độ.
Ký hiệu hình bình hành thường dùng là: ABCD, với điều kiện AB // CD và AD // BC.
Các tính chất cơ bản của hình bình hành
Hình bình hành có nhiều tính chất đặc trưng, giúp phân biệt với các hình khác và áp dụng trong các dạng bài tập khác nhau. Dưới đây là những tính chất cơ bản nhất:
Cạnh đối song song và bằng nhau:
AB // CD và AB = CD
AD // BC và AD = BC
Góc đối bằng nhau:
∠A = ∠C
∠B = ∠D
Hai đường chéo cắt nhau tại trung điểm mỗi đường:
Gọi O là giao điểm hai đường chéo AC và BD
⇒ O là trung điểm của AC và BD
⇒ AO = OC và BO = OD
Tổng hai góc kề nhau bằng 180°:
∠A + ∠B = 180°
∠B + ∠C = 180° (và tương tự với các cặp góc còn lại)
Diện tích hình bình hành:
Diện tích S được tính theo công thức:
S = a × h
Trong đó:
a là độ dài cạnh đáy
h là chiều cao ứng với cạnh đáy đó

Học sinh trong giờ toánĐể xác định một tứ giác là hình bình hành, có thể sử dụng một trong các tiêu chí nhận biết dưới đây:
Dựa trên song song:
Một tứ giác có hai cặp cạnh đối song song ⇒ là hình bình hành
Dựa trên độ dài cạnh:
Một tứ giác có hai cặp cạnh đối bằng nhau ⇒ là hình bình hành
Một tứ giác có hai cạnh đối vừa song song vừa bằng nhau ⇒ là hình bình hành
Dựa trên góc:
Một tứ giác có hai góc đối bằng nhau ⇒ là hình bình hành
(kết hợp với điều kiện khác để đủ chứng minh)
Dựa trên đường chéo:
Một tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ là hình bình hành
Trong hệ tọa độ Oxy:
Giả sử có tứ giác ABCD với tọa độ các điểm đã biết, ta có thể chứng minh hình bình hành bằng cách:
Kiểm tra vector: AB = CD và AD = BC
Kiểm tra tọa độ trung điểm của hai đường chéo trùng nhau
Ví dụ:
Nếu A(0, 0), B(2, 3), C(6, 3), D(4, 0), thì có thể tính trung điểm AC và BD đều là (3, 1.5) ⇒ ABCD là hình bình hành.
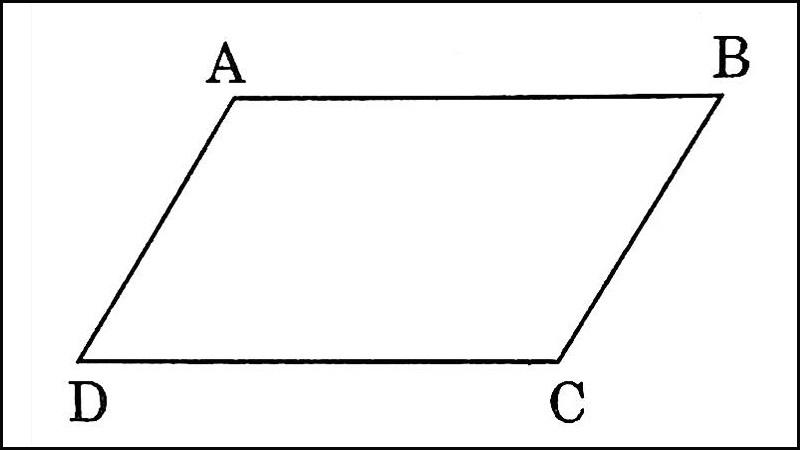
Hình bình hành
Tính chất hình bình hành được sử dụng rất nhiều trong các dạng bài tập toán học, đặc biệt ở chương trình Toán lớp 8 và Toán 9. Một số ứng dụng tiêu biểu như:
Tính độ dài cạnh, chiều cao, diện tích:
Áp dụng công thức diện tích S = a × h hoặc sử dụng định lý Pythagore nếu biết tọa độ hoặc độ dài.
Chứng minh một hình là hình bình hành:
Dựa vào điều kiện song song, bằng nhau, góc, vector hoặc trung điểm.
Tìm tọa độ điểm còn thiếu:
Cho ba đỉnh của hình bình hành, có thể tìm tọa độ đỉnh thứ tư bằng công thức vector:
Giả sử biết A, B, C ⇒ D = B + (C - A)
Chứng minh đẳng thức vector:
AB + DC = 0 hoặc AB = DC (cùng phương, cùng độ dài và chiều ngược nhau)
Giải các bài toán liên quan đến tam giác, đường trung bình:
Hình bình hành thường được sử dụng trong chứng minh các đường trung bình, tam giác đồng dạng, hoặc tam giác vuông trong hình học không gian.
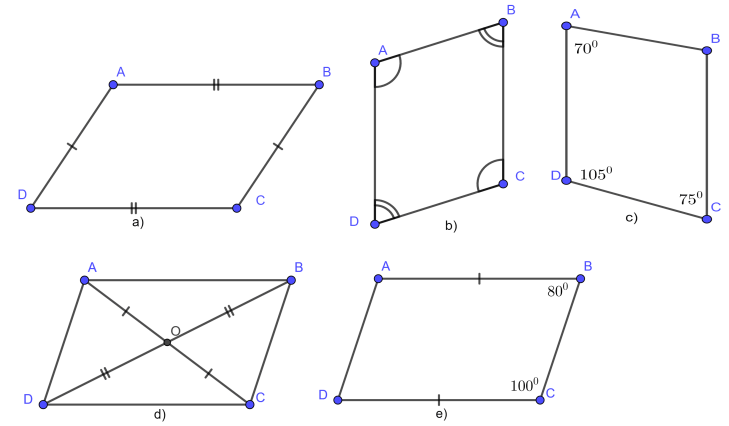
Các tính chất của hình bình hành
>> Xem thêm: Công thức lượng giác 11
Hình bình hành tuy đơn giản nhưng có nhiều tính chất, để ghi nhớ dễ dàng hơn, bạn có thể áp dụng các mẹo sau:
Gợi nhớ bằng hình ảnh:
Hãy tưởng tượng hình bình hành là một hình chữ nhật bị nghiêng. Từ đó, bạn sẽ dễ nhớ các cặp cạnh đối song song, các góc đối bằng nhau, và đường chéo cắt nhau tại trung điểm.
Dùng từ khóa viết tắt:
CB: Cạnh Bằng nhau
SS: Song Song
GD: Góc Đối bằng nhau
DC: Đường Chéo cắt tại trung điểm
TS: Tổng góc kề bằng 180°
Chỉ cần nhớ các chữ cái đầu tiên này, bạn có thể hệ thống hóa toàn bộ tính chất.
Vẽ sơ đồ tư duy:
Ghi ở giữa là "Hình bình hành", sau đó vẽ các nhánh phụ:
Cạnh
Góc
Đường chéo
Diện tích
Dấu hiệu nhận biết
→ Điều này giúp bạn học và ôn tập cực kỳ hiệu quả.
Kết luận
Hình bình hành là một trong những hình cơ bản nhưng rất quan trọng trong chương trình học toán trung học cơ sở. Việc nắm vững khái niệm, tính chất và dấu hiệu nhận biết hình bình hành không chỉ giúp bạn giải nhanh các bài toán hình học mà còn hỗ trợ hiệu quả trong học hình tọa độ.
Hãy thường xuyên luyện tập các bài tập thực hành, vẽ hình, sử dụng sơ đồ tư duy và áp dụng mẹo ghi nhớ để thành thạo phần kiến thức tính chất hình bình hành. Việc hiểu và ghi nhớ đúng bản chất của hình bình hành sẽ giúp bạn chinh phục mọi dạng bài liên quan trong đề thi và kiểm tra.
>> Tham khảo: Taxi hà nội đi nội bài giá rẻ