Công thức lượng giác 11
Lượng giác là chuyên đề quan trọng trong chương trình Toán lớp 11, cung cấp kiến thức nền tảng cho các môn học khác như hình học, giải tích, cũng như các ứng dụng trong thực tế như vật lý, kỹ thuật. Trong lớp 11, học sinh được làm quen với các hàm lượng giác cơ bản, các công thức lượng giác 11 quan trọng và phương pháp khai triển, biến đổi biểu thức lượng giác.
Việc nắm vững chuyên đề lượng giác giúp học sinh giải bài tập nhanh hơn, hiểu sâu hơn các dạng toán khó và chuẩn bị tốt cho các kỳ thi quan trọng như THPT Quốc gia.
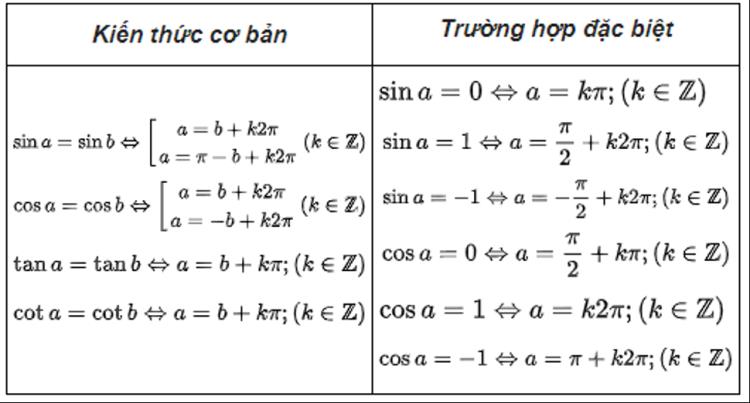Kiến thúc cơ bản của công thứcCác công thức lượng giác lớp 11 quan trọng cần ghi nhớ
Dưới đây là các công thức lượng giác cơ bản và mở rộng quan trọng nhất trong chương trình lớp 11
Công thức cơ bản:
sin² x + cos² x = 1
1 + tan² x = 1 / cos² x
1 + cot² x = 1 / sin² x
Công thức cộng:
sin(a ± b) = sin a × cos b ± cos a × sin b
cos(a ± b) = cos a × cos b ∓ sin a × sin b
tan(a ± b) = (tan a ± tan b) / (1 ∓ tan a × tan b)
Công thức nhân đôi:
sin 2a = 2 × sin a × cos a
cos 2a = cos² a − sin² a = 2 × cos² a − 1 = 1 − 2 × sin² a
tan 2a = (2 × tan a) / (1 − tan² a)
Công thức hạ bậc:
sin² a = (1 − cos 2a) / 2
cos² a = (1 + cos 2a) / 2
Công thức biến đổi tổng thành tích:
sin a + sin b = 2 × sin((a + b)/2) × cos((a − b)/2)
sin a − sin b = 2 × cos((a + b)/2) × sin((a − b)/2)
cos a + cos b = 2 × cos((a + b)/2) × cos((a − b)/2)
cos a − cos b = −2 × sin((a + b)/2) × sin((a − b)/2)
Việc ghi nhớ các công thức này là nền tảng để học sinh làm tốt các bài tập lượng giác và thi cử hiệu quả.
Học sinh trong giờ thi
Để học sinh tiện theo dõi và ôn tập, dưới đây là bảng tổng hợp công thức lượng giác lớp 11 ở dạng thuần văn bản
|
Loại công thức
|
Công thức
|
|
Công thức cơ bản
|
sin² x + cos² x = 1
|
|
1 + tan² x = 1 / cos² x
|
|
1 + cot² x = 1 / sin² x
|
|
Công thức cộng
|
sin(a ± b) = sin a × cos b ± cos a × sin b
|
|
cos(a ± b) = cos a × cos b ∓ sin a × sin b
|
|
tan(a ± b) = (tan a ± tan b) / (1 ∓ tan a × tan b)
|
|
Công thức nhân đôi
|
sin 2a = 2 × sin a × cos a
|
|
cos 2a = cos² a − sin² a
|
|
cos 2a = 2 × cos² a − 1
|
|
cos 2a = 1 − 2 × sin² a
|
|
tan 2a = (2 × tan a) / (1 − tan² a)
|
|
Công thức hạ bậc
|
sin² a = (1 − cos 2a) / 2
|
|
cos² a = (1 + cos 2a) / 2
|
|
Công thức biến đổi tổng thành tích
|
sin a + sin b = 2 × sin((a + b)/2) × cos((a − b)/2)
|
|
sin a − sin b = 2 × cos((a + b)/2) × sin((a − b)/2)
|
|
cos a + cos b = 2 × cos((a + b)/2) × cos((a − b)/2)
|
|
cos a − cos b = −2 × sin((a + b)/2) × sin((a − b)/2)
|
Việc học thuộc công thức lượng giác là thách thức với nhiều học sinh, dưới đây là một số mẹo giúp học nhanh và nhớ lâu:
Phân loại công thức theo nhóm: cơ bản, cộng, nhân đôi, hạ bậc để dễ nhớ.
Viết lại công thức nhiều lần trên giấy, vừa viết vừa đọc to.
Sử dụng sơ đồ tư duy hoặc bảng tổng hợp giúp hệ thống kiến thức.
Áp dụng ngay công thức vào bài tập cụ thể để hiểu rõ cách dùng.
Dùng các câu thơ, câu khẩu quyết hoặc mnemotechnics để nhớ.
Ôn tập định kỳ, tránh học dồn một lúc rồi quên nhanh.
Áp dụng những phương pháp này sẽ giúp việc học lượng giác dễ dàng và hiệu quả hơn rất nhiều.
Ứng dụng vào nhiều lĩnh vựcCông thức lượng giác 11 không chỉ giúp giải các bài toán trên lớp mà còn ứng dụng trong nhiều dạng bài khác nhau:
Rút gọn biểu thức lượng giác phức tạp.
Chứng minh đẳng thức lượng giác.
Giải phương trình lượng giác.
Tính toán góc, cạnh trong các bài toán hình học.
Áp dụng trong vật lý, kỹ thuật để mô tả các hiện tượng dao động, sóng.
Việc luyện tập đa dạng các dạng bài tập sẽ giúp học sinh nâng cao tư duy và khả năng vận dụng công thức hiệu quả.
Chuyên đề lượng giác 11 với hệ thống công thức đầy đủ và cách học thông minh sẽ giúp học sinh không những vượt qua các bài tập lượng giác khó mà còn xây dựng nền tảng kiến thức chắc chắn cho các môn học liên quan.
Bạn có thể lưu lại bảng công thức lượng giác 11 trên và kết hợp luyện tập để học lượng giác hiệu quả hơn.