Tính chất hình bình hành
Hình bình hành là gì?
Trong hình học, hình bình hành là một tứ giác có hai cặp cạnh đối song song và bằng nhau. Hình bình hành có thể xuất hiện trong nhiều tình huống và bài toán khác nhau, từ các bài toán đơn giản trong sách giáo khoa đến các ứng dụng phức tạp trong kiến trúc, kỹ thuật và vật lý. Các tính chất hình bình hành rất quan trọng trong việc giải quyết các bài toán liên quan đến tứ giác, đặc biệt là các bài toán về diện tích, góc, và các quan hệ giữa các đoạn thẳng.
Hình bình hành có thể nhận diện thông qua các đặc điểm dễ nhận thấy như cặp cạnh đối song song và bằng nhau. Điều này giúp chúng ta dễ dàng nhận diện nó trong các bài toán hình học. Việc hiểu rõ về các tính chất này sẽ giúp bạn giải quyết các bài toán và ứng dụng hình học một cách hiệu quả.
Hình bình hànhTính chất 1: Cặp cạnh đối song song và bằng nhau
Một trong những tính chất cơ bản và quan trọng nhất của hình bình hành là các cặp cạnh đối song song và bằng nhau. Điều này có nghĩa là hai cạnh đối diện của hình bình hành sẽ song song với nhau và có độ dài bằng nhau. Tính chất này giúp chúng ta dễ dàng nhận diện hình bình hành trong các bài toán và hình vẽ.
Cụ thể, giả sử bạn có một hình bình hành với bốn đỉnh A, B, C, D, thì hai cặp cạnh đối là AB và CD song song và có chiều dài bằng nhau, tương tự với AD và BC. Điều này là đặc điểm đặc trưng giúp hình bình hành phân biệt với các tứ giác khác.
Tính chất 2: Các góc đối diện bằng nhau
Một tính chất quan trọng khác của hình bình hành là các góc đối diện của hình bình hành luôn bằng nhau. Nếu bạn xét các góc tại các đỉnh A, B, C, D của hình bình hành, thì bạn sẽ nhận thấy rằng góc ∠A và góc ∠C bằng nhau, và góc ∠B và góc ∠D cũng bằng nhau.
Tính chất này giúp bạn có thể tính toán góc khi có dữ liệu về một trong các góc của hình bình hành, từ đó dễ dàng suy ra các góc còn lại. Nó cũng là một trong những lý thuyết quan trọng trong việc áp dụng hình học vào giải các bài toán cụ thể.
Tính chất 3: Các đường chéo cắt nhau tại trung điểm
Hình bình hành cũng có tính chất đặc biệt về các đường chéo. Các đường chéo của hình bình hành sẽ cắt nhau tại trung điểm của mỗi đường. Điều này có nghĩa là nếu bạn vẽ hai đường chéo của một hình bình hành, điểm giao nhau của chúng sẽ chia mỗi đường chéo thành hai đoạn thẳng có độ dài bằng nhau.
Tính chất này rất quan trọng khi bạn cần giải các bài toán về các đoạn thẳng trong hình học, đặc biệt là khi yêu cầu tính toán diện tích hoặc chiều dài các đoạn thẳng.
Tính chất 4: Diện tích hình bình hành
Diện tích của hình bình hành có thể tính bằng công thức:
Diện tích = Cạnh đáy × Chiều cao
Trong đó, cạnh đáy là độ dài một trong các cạnh của hình bình hành và chiều cao là khoảng cách vuông góc từ đáy đến cạnh đối diện. Tính chất này giúp bạn dễ dàng tính diện tích của hình bình hành trong các bài toán thực tế hoặc toán học.
Tham khảo: Công thức lượng giác 11
Ứng dụng trong toán học
Trong toán học, hình bình hành xuất hiện rất nhiều trong các bài toán liên quan đến hình học, đặc biệt là trong các bài toán về diện tích, chu vi và tính chất của các tứ giác. Các tính chất về cạnh song song, góc đối diện bằng nhau, và các đường chéo cắt nhau tại trung điểm giúp chúng ta dễ dàng giải quyết các bài toán phức tạp.
Hình bình hành cũng là cơ sở để xây dựng các khái niệm hình học khác, như hình vuông, hình chữ nhật, và hình thoi. Việc nắm vững tính chất của hình bình hành sẽ giúp bạn hiểu rõ hơn về các hình học khác và giải quyết các bài toán hình học một cách dễ dàng.
Ứng dụng trong thực tế
Ngoài các bài toán toán học, hình bình hành còn có nhiều ứng dụng trong thực tế. Ví dụ, trong kiến trúc, các kiến trúc sư có thể sử dụng hình bình hành để thiết kế các cấu trúc có dạng tứ giác với các tính chất đối song song. Bên cạnh đó, hình bình hành cũng xuất hiện trong các lĩnh vực như kỹ thuật, vẽ tranh, và thậm chí trong việc thiết kế các vật dụng hàng ngày.
Việc hiểu rõ về hình bình hành và các tính chất của nó giúp bạn có thể áp dụng kiến thức này vào việc giải quyết các vấn đề trong thực tế, từ thiết kế đồ vật đến xây dựng các công trình.
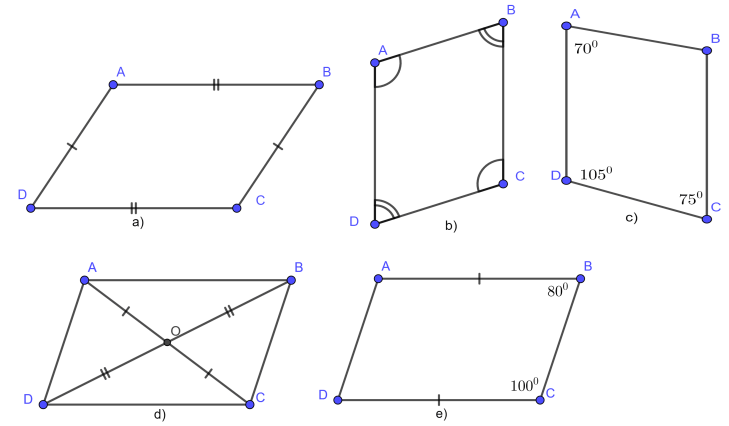
Tính chất của hình bình hành được áp dụng trong các bài toán toán học và thực tếBước 1: Xác định các tính chất của hình bình hành
Trước khi bắt đầu giải bài toán, bạn cần xác định các tính chất cơ bản của hình bình hành trong bài toán. Các tính chất như các cặp cạnh đối song song, các góc đối diện bằng nhau, các đường chéo cắt nhau tại trung điểm là những yếu tố quan trọng mà bạn cần lưu ý.
Bước 2: Áp dụng công thức tính diện tích và chu vi
Khi bài toán yêu cầu tính diện tích hoặc chu vi của hình bình hành, bạn chỉ cần áp dụng công thức:
Diện tích = Cạnh đáy × Chiều cao
Chu vi = 2 × (Cạnh đáy + Cạnh cao)
Các công thức này sẽ giúp bạn giải quyết bài toán nhanh chóng và chính xác.
Bước 3: Sử dụng tính chất đường chéo
Nếu bài toán liên quan đến các đoạn thẳng và đường chéo của hình bình hành, bạn cần nhớ rằng các đường chéo của hình bình hành cắt nhau tại trung điểm. Điều này giúp bạn tính toán chính xác độ dài các đoạn thẳng trong bài toán.
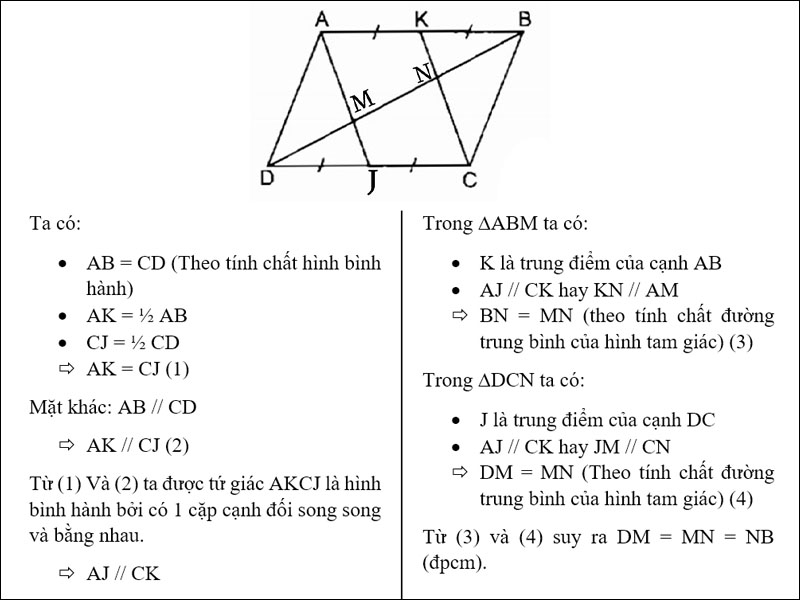
Giải bài toán về hình bình hành trong các bài toán hình họcHình bình hành là một trong những hình học cơ bản và quan trọng trong toán học. Việc hiểu và áp dụng các tính chất hình bình hành sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về hình bình hành và các ứng dụng của nó trong toán học cũng như thực tế.