Công thức lượng giác 11
Trước khi đi sâu vào các công thức lượng giác lớp 11, chúng ta hãy cùng nhau củng cố lại những kiến thức căn bản. Việc xây dựng một nền tảng vững chắc sẽ là điều kiện tiên quyết để bạn tiếp cận những công thức phức tạp hơn một cách dễ dàng và chính xác. Dù bạn mới bắt đầu hay đang ôn tập lại, phần này sẽ giúp bạn tự tin hơn khi giải các bài toán trong chương trình lớp 11.
Hiểu đúng khái niệm góc và đơn vị đo
Một trong những điều đầu tiên bạn cần ghi nhớ khi học lượng giác là hiểu rõ về góc và các đơn vị đo góc. Góc có thể được biểu diễn bằng độ hoặc radian – hai đơn vị phổ biến trong chương trình học. Việc linh hoạt chuyển đổi giữa hai đơn vị này sẽ giúp bạn xử lý nhanh gọn nhiều dạng bài khác nhau. Ví dụ, bạn nên nhớ rằng 180 độ tương đương với pi radian. Đây là kiến thức nền tảng, bởi nó xuất hiện xuyên suốt trong các công thức và bài toán lượng giác.
Vòng tròn lượng giác và vai trò của nó
Tiếp theo, chúng ta không thể không nhắc đến vòng tròn lượng giác – một công cụ trực quan giúp bạn hình dung rõ ràng hơn về các giá trị lượng giác của các góc. Khi nắm chắc vòng tròn lượng giác, bạn sẽ dễ dàng xác định được dấu của các hàm lượng giác trong từng góc phần tư, từ đó tránh được những sai lầm không đáng có. Đặc biệt, nó còn giúp bạn hiểu sâu hơn về quy luật biến thiên của sin, cos, tan,... và là nền tảng để giải các phương trình liên quan.
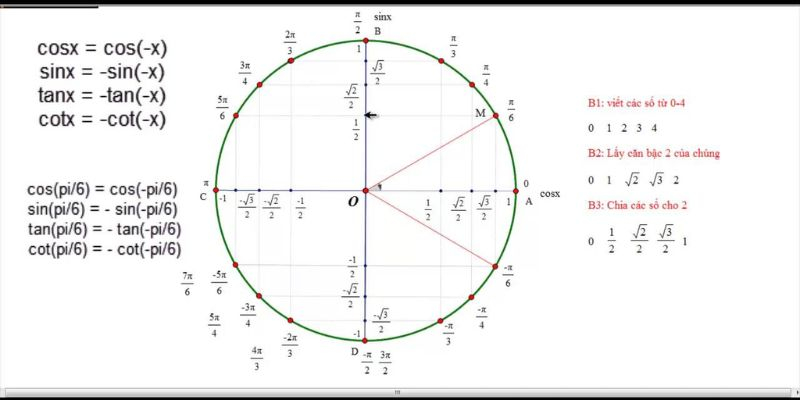
Vòng tròn lượng giácSau khi đã trang bị kiến thức nền, bạn sẽ bắt đầu bước vào phần trọng tâm nhất – các công thức lượng giác lớp 11. Đây chính là phần nội dung mà mọi học sinh cần nắm vững để làm chủ chương trình Toán học lớp 11. Việc hiểu rõ và ghi nhớ các công thức này không chỉ giúp bạn làm bài nhanh hơn mà còn giúp phát triển tư duy logic toán học một cách đáng kể.
Công thức cộng góc và biến đổi tích thành tổng
Trong quá trình học, bạn sẽ gặp những biểu thức chứa tổng hoặc hiệu các góc như a + b hoặc a - b. Lúc này, công thức cộng góc chính là công cụ giúp bạn xử lý các biểu thức này một cách dễ dàng. Ví dụ:
sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
Sự hiểu biết và thành thạo trong việc áp dụng các công thức này sẽ hỗ trợ bạn rút gọn biểu thức hoặc giải phương trình lượng giác một cách hiệu quả.
Công thức nhân đôi và nhân ba góc
Không dừng lại ở đó, bạn còn cần làm quen với các công thức nhân đôi và nhân ba góc. Đây là những công thức mở rộng thường xuyên xuất hiện trong các đề thi:
sin(2a) = 2sin(a)cos(a)
cos(2a) = cos^2(a) - sin^2(a)
Chúng ta sử dụng chúng để biến đổi biểu thức, chứng minh các đẳng thức và rút gọn phương trình một cách linh hoạt. Việc nắm chắc các công thức này sẽ giúp bạn tiết kiệm thời gian khi làm bài và tránh được những lỗi thường gặp.
Tham khảo: Tính chất hình bình hành

Công thức lượng giác đầy đủHọc lý thuyết thôi chưa đủ, điều quan trọng là bạn cần biết cách vận dụng các công thức lượng giác 11 để giải các phương trình. Dưới đây là những dạng bài tiêu biểu giúp bạn làm quen với cách ứng dụng kiến thức một cách hiệu quả.
Giải phương trình lượng giác cơ bản
Khi bắt đầu làm quen với phương trình lượng giác, bạn sẽ thường xuyên gặp các dạng đơn giản như sin(x) = a hoặc cos(x) = b. Để giải được những phương trình này, bạn cần hiểu rõ tính tuần hoàn, chu kỳ và tập xác định của các hàm lượng giác. Việc xác định nghiệm tổng quát và nghiệm riêng sẽ trở nên dễ dàng nếu bạn nắm chắc các quy tắc này.
Biến đổi phương trình về dạng quen thuộc
Không phải mọi phương trình lượng giác đều được cho sẵn ở dạng đơn giản. Nhiều bài toán đòi hỏi bạn phải biến đổi chúng về dạng quen thuộc trước khi giải. Ví dụ, bạn có thể sử dụng đẳng thức cơ bản:
cos^2(x) + sin^2(x) = 1
Đây là công thức mà bạn nên thuộc nằm lòng, bởi nó giúp đơn giản hóa nhiều biểu thức phức tạp và rút gọn phương trình hiệu quả. Hãy luyện tập biến đổi linh hoạt giữa các công thức để nắm chắc kỹ năng giải toán.
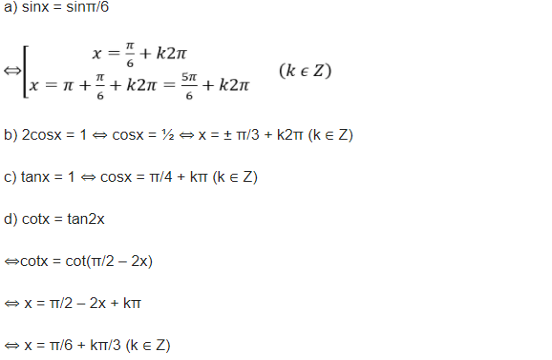
Bài tập cơ bản về lượng giácĐứng trước hàng loạt công thức cần nhớ, không ít bạn cảm thấy quá tải và lo lắng. Tuy nhiên, đừng vội nản lòng. Với một số phương pháp học tập hợp lý và khoa học, bạn hoàn toàn có thể ghi nhớ và sử dụng thành thạo các công thức lượng giác lớp 11.
Sử dụng sơ đồ tư duy và bảng tóm tắt
Một trong những cách học hiệu quả là lập sơ đồ tư duy để hệ thống hóa kiến thức. Việc sắp xếp công thức theo nhóm, theo tính chất tương đồng sẽ giúp bạn ghi nhớ lâu hơn và dễ dàng tra cứu khi cần thiết. Ngoài ra, bạn cũng có thể tự tay làm bảng tóm tắt để ôn tập nhanh trước mỗi bài kiểm tra hoặc kỳ thi.
Thực hành thường xuyên qua bài tập đa dạng
Dù bạn đã học kỹ lý thuyết đến đâu, thì việc làm bài tập vẫn là yếu tố quyết định giúp bạn hiểu sâu và ghi nhớ lâu. Hãy chủ động chia nhỏ các dạng bài theo từng chuyên đề và luyện tập dần từ cơ bản đến nâng cao. Quá trình rèn luyện này sẽ giúp bạn phát hiện được điểm yếu và từ đó cải thiện từng chút một.
Tóm lại, công thức lượng giác lớp 11 là phần kiến thức quan trọng không thể thiếu trong hành trình học Toán THPT của bạn. Việc nắm chắc và áp dụng thành thạo các công thức này không chỉ giúp bạn đạt điểm cao trong các kỳ thi mà còn tạo nền tảng vững chắc để học tốt hơn ở các lớp sau. Đừng quên luyện tập thường xuyên, kết hợp nhiều phương pháp học tập thông minh và chia sẻ kiến thức cùng bạn bè. Nếu bạn thấy bài viết hữu ích, hãy lưu lại và lan tỏa để cùng nhau học tốt hơn nhé!
>> Tham khảo: Dịch vụ taxi đi sân bay nội bài