Nhị thức Newton
Trong thế giới rộng lớn của toán học, việc khai triển các biểu thức đại số lũy thừa cao thường là một thách thức không nhỏ nếu chỉ sử dụng các phép nhân thông thường. Thật may mắn, chúng ta có một công cụ vô cùng mạnh mẽ và hiệu quả để giải quyết vấn đề này, đó chính là khai triển lũy thừa của tổng. Định lý toán học kinh điển này không chỉ giúp đơn giản hóa các phép tính phức tạp mà còn mở ra cánh cửa đến nhiều lĩnh vực ứng dụng quan trọng khác.
Để có thể sử dụng và hiểu rõ một công cụ toán học, điều quan trọng đầu tiên là phải nắm bắt được bản chất và nguồn gốc của nó. Nhị thức newton không phải là một khái niệm ngẫu nhiên xuất hiện, mà là kết quả của quá trình nghiên cứu và phát triển kéo dài, mang lại một định lý toán học có ý nghĩa sâu sắc.
Lịch sử phát triển của khai triển lũy thừa của tổng gắn liền với tên tuổi của nhà bác học vĩ đại Isaac Newton. Mặc dù các trường hợp đặc biệt của việc khai triển nhị thức (như (a+b)^2 hay (a+b)^3) đã được biết đến từ rất lâu, chính Newton là người đã tổng quát hóa công thức này cho mọi số mũ nguyên dương n. Công trình của ông, đặc biệt là trong cuốn "Principia Mathematica" năm 1687, đã trình bày một phiên bản mở rộng của định lý nhị thức, cho phép khai triển không chỉ với số mũ nguyên dương mà còn với số mũ âm và số mũ phân số, mặc dù bài viết này chủ yếu tập trung vào trường hợp số mũ nguyên dương. Sự ra đời của khai triển lũy thừa của tổng đã đánh dấu một bước tiến quan trọng trong đại số, cung cấp một nền tảng vững chắc cho nhiều phát triển toán học sau này, bao gồm cả giải tích. Việc hiểu rõ định nghĩa và bối cảnh lịch sử này giúp chúng ta trân trọng hơn giá trị và sức mạnh của khai triển lũy thừa của tổng khi áp dụng nó vào giải quyết các bài toán.
Khai triển lũy thừa của tổng là một trong những định lý quan trọng trong đại số tổ hợp, cho phép khai triển biểu thức có dạng (a + b)^n thành một tổng các số hạng chứa lũy thừa của a và b. Mỗi số hạng trong khai triển bao gồm một hệ số gọi là hệ số nhị thức, được tính bằng tổ hợp chập k của n phần tử, ký hiệu là C(n, k). Công thức này được phát triển bởi nhà toán học Isaac Newton vào thế kỷ 17 và đã trở thành một công cụ thiết yếu trong nhiều lĩnh vực khoa học và kỹ thuật.
Tham khảo: Công thức lượng giác 11

Issac NewtonĐịnh nghĩa và công thức tổng quát
Công thức khai triển lũy thừa của tổng cho phép khai triển biểu thức (a + b)^n như sau:
(a + b)^n = C(n, 0) * a^n * b^0 + C(n, 1) * a^(n-1) * b^1 + ... + C(n, n) * a^0 * b^n
Trong đó, C(n, k) là hệ số nhị thức, được tính bằng công thức:
C(n, k) = n! / (k! * (n - k)!)
Mỗi số hạng trong khai triển bao gồm một hệ số nhị thức và các lũy thừa của a và b sao cho tổng số mũ bằng n.
Tính chất của khai triển lũy thừa của tổng
Số lượng số hạng trong khai triển là n + 1.
Tổng số mũ của a và b trong mỗi số hạng luôn bằng n.
Các hệ số nhị thức có tính đối xứng: C(n, k) = C(n, n - k).
Tổng các hệ số trong khai triển (a + b)^n bằng 2^n khi a = b = 1.
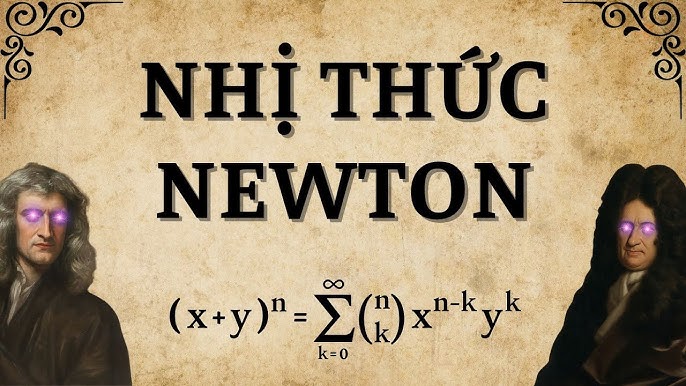
Công thức nhị thức mang tên NewtonCấu trúc của tam giác Pascal
Tam giác Pascal là một cấu trúc số học sắp xếp các hệ số nhị thức theo dạng tam giác. Mỗi hàng trong tam giác tương ứng với các hệ số trong khai triển của (a + b)^n. Cụ thể, hàng thứ n trong tam giác chứa các hệ số C(n, 0), C(n, 1), ..., C(n, n).
Mối liên hệ với khai triển lũy thừa của tổng
Tam giác Pascal cung cấp một cách trực quan để xác định các hệ số trong khai triển khai triển lũy thừa của tổng. Ví dụ, để khai triển (a + b)^4, ta lấy hàng thứ 4 trong tam giác Pascal: 1, 4, 6, 4, 1. Do đó, khai triển là:
(a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4

Tam giác PascalTrong toán học và xác suất
Khai triển lũy thừa của tổng là nền tảng trong các lĩnh vực tổ hợp và xác suất. Nó giúp tính toán số lượng tổ hợp, xác suất của các sự kiện và phân tích các chuỗi số. Ví dụ, trong xác suất, công thức nhị thức được sử dụng để tính xác suất của k lần thành công trong n lần thử nghiệm độc lập.
Trong khoa học máy tính và kỹ thuật
Trong khoa học máy tính, nhị thức Newton được áp dụng trong các thuật toán phân tích độ phức tạp và trong việc phát triển các thuật toán hiệu quả. Trong kỹ thuật, nó được sử dụng để mô hình hóa và phân tích các hệ thống, đặc biệt trong lĩnh vực điện tử và cơ khí.
Trong tài chính và kinh tế
Khai triển lũy thừa của tổng giúp mô hình hóa các kịch bản tài chính, như tính toán lãi suất kép và phân tích rủi ro đầu tư. Nó cũng được sử dụng trong các mô hình kinh tế để dự đoán xu hướng và phân tích dữ liệu.
>> Tham khảo: Taxi đi sân bay nội bài
Tìm hệ số của một số hạng cụ thể
Để tìm hệ số của số hạng chứa a^k * b^(n - k) trong khai triển (a + b)^n, ta sử dụng công thức:
Hệ số = C(n, k)
Ví dụ, trong khai triển (x + y)^5, hệ số của x^3 * y^2 là:
C(5, 3) = 10
Tính tổng các hệ số trong khai triển
Để tính tổng các hệ số trong khai triển (a + b)^n, ta đặt a = b = 1:
Tổng = (1 + 1)^n = 2^n
Ví dụ, tổng các hệ số trong khai triển (x + y)^3 là:
2^3 = 8
Khai triển lũy thừa của tổng là một công cụ toán học mạnh mẽ, không chỉ hữu ích trong việc khai triển các biểu thức lũy thừa mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và đời sống. Việc nắm vững công thức và các tính chất của nhị thức Newton sẽ giúp bạn giải quyết hiệu quả các bài toán phức tạp và áp dụng vào thực tiễn một cách linh hoạt.