Công thức lượng giác 11
Tầm quan trọng của công thức lượng giác trong chương trình lớp 11
Lượng giác là một phần quan trọng trong chương trình Toán lớp 11, đóng vai trò nền tảng cho nhiều kiến thức nâng cao sau này. Các công thức lượng giác không chỉ giúp học sinh giải quyết các bài toán có liên quan đến góc, tam giác mà còn là công cụ hỗ trợ trong các bài toán hình học và giải phương trình. Khi nắm vững các công thức này, học sinh sẽ dễ dàng tiếp cận và giải quyết được các bài toán khó trong chương trình học và trong các kỳ thi.
Các công thức lượng giác trong lớp 11 là nền tảng cho các bài toán lượng giác sau này. Vì vậy, việc nắm vững chúng không chỉ giúp học sinh hiểu rõ lý thuyết mà còn có thể ứng dụng vào các bài tập thực tế trong học tập. Đặc biệt, với các bài thi quan trọng như kỳ thi THPT Quốc gia, công thức lượng giác chính là chìa khóa giúp học sinh giải quyết nhanh và chính xác các bài toán trong đề thi.
Bài viết này nhằm cung cấp cho bạn cái nhìn tổng quan về các công thức lượng giác 11 quan trọng, giúp bạn hiểu rõ và áp dụng chúng trong học tập. Chúng tôi sẽ trình bày các công thức một cách dễ hiểu, kèm theo hình ảnh minh họa và liên kết đến các bài viết liên quan để bạn có thể tìm hiểu thêm các vấn đề nâng cao khác.
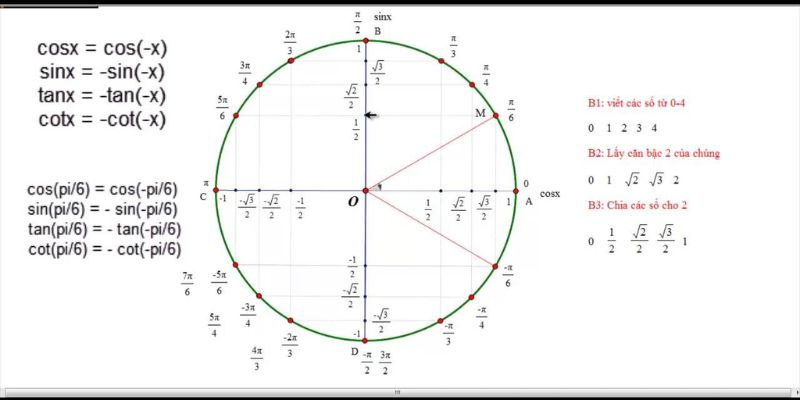
Vòng tròn lượng giácĐịnh nghĩa các hàm lượng giác
Lượng giác là một nhánh của toán học nghiên cứu về các mối quan hệ giữa các góc và cạnh trong tam giác, đặc biệt là tam giác vuông. Các hàm lượng giác được sử dụng để mô tả các mối quan hệ này, và chúng thường xuất hiện trong các bài toán về góc và chiều dài các cạnh của tam giác.
Trong tam giác vuông, các hàm lượng giác được định nghĩa như sau:
sin(θ): tỉ số giữa cạnh đối diện với góc θ và cạnh huyền của tam giác vuông.
cos(θ): tỉ số giữa cạnh kề với góc θ và cạnh huyền của tam giác vuông.
tan(θ): tỉ số giữa cạnh đối diện với góc θ và cạnh kề của tam giác vuông.
cot(θ): tỉ số giữa cạnh kề với góc θ và cạnh đối diện của tam giác vuông.
Việc hiểu rõ các định nghĩa này là bước đầu tiên để nắm vững công thức lượng giác 11, giúp bạn có thể vận dụng vào các bài toán khác nhau.
Các công thức cơ bản
Một trong những công thức quan trọng và dễ nhớ trong chương trình lớp 11 là công thức Pythagoras, giúp bạn tính toán các giá trị của các hàm lượng giác. Các công thức cơ bản bao gồm:
sin²(θ) + cos²(θ) = 1
1 + tan²(θ) = 1 / cos²(θ)
1 + cot²(θ) = 1 / sin²(θ)
Những công thức này là nền tảng giúp bạn giải quyết các bài toán lượng giác trong chương trình công thức lượng giác 11. Việc áp dụng đúng các công thức này sẽ giúp bạn tính toán chính xác các giá trị của các hàm lượng giác trong mọi trường hợp.
Tham khảo: Bảng phối màu quần áo

Các hàm lượng giác cơ bản trong chương trình lớp 11Công thức cộng và trừ
Một trong những công thức quan trọng trong lượng giác là công thức cộng và trừ, giúp bạn tính giá trị của các hàm lượng giác khi biết tổng hoặc hiệu của hai góc. Đây là công thức được áp dụng phổ biến trong các bài toán về góc và các bài toán liên quan đến các tính toán lượng giác.
sin(a ± b) = sin(a)cos(b) ± cos(a)sin(b)
cos(a ± b) = cos(a)cos(b) ∓ sin(a)sin(b)
tan(a ± b) = (tan(a) ± tan(b)) / (1 ∓ tan(a)tan(b))
Công thức nhân đôi và nhân ba
Các công thức nhân đôi và nhân ba được sử dụng để tính giá trị của các hàm lượng giác khi góc được nhân lên. Những công thức này đặc biệt hữu ích trong các bài toán về các góc lớn hơn 90 độ hoặc các góc phức tạp. Việc nắm vững công thức này sẽ giúp bạn giải quyết nhanh chóng các bài toán lượng giác.
sin(2a) = 2sin(a)cos(a)
cos(2a) = cos²(a) - sin²(a)
tan(2a) = 2tan(a) / (1 - tan²(a))
Việc áp dụng các công thức này sẽ giúp bạn tính toán được giá trị của các hàm lượng giác cho các góc lớn hoặc các bài toán có chứa các hàm số lượng giác phức tạp.
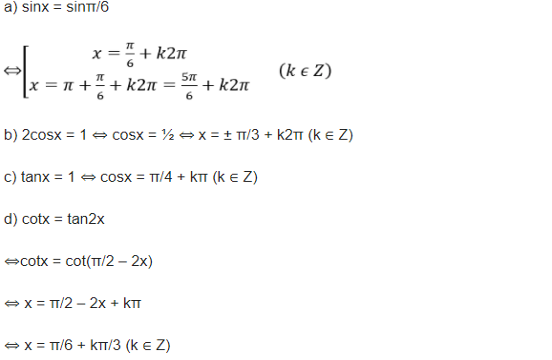
Công thức lượng giác nâng cao trong chương trình lớp 11Giải phương trình lượng giác
Phương trình lượng giác là một phần quan trọng trong các bài toán lượng giác. Bằng cách sử dụng các công thức lượng giác 11, bạn có thể giải các phương trình có chứa các hàm lượng giác như sin, cos, tan, cot, v.v.
Ví dụ, bạn có thể giải phương trình sau bằng cách áp dụng các công thức lượng giác đã học:
sin(x) = a
cos(x) = b
tan(x) = c
Việc sử dụng các công thức và quy trình giải phương trình lượng giác đúng cách sẽ giúp bạn tìm ra nghiệm của phương trình một cách chính xác.
Ứng dụng trong hình học
Các công thức lượng giác còn được sử dụng để tính độ dài cạnh, diện tích và góc trong tam giác. Ví dụ, trong một tam giác vuông, bạn có thể sử dụng định lý sin hoặc định lý cos để tính các cạnh hoặc góc chưa biết.
a / sin(A) = b / sin(B) = c / sin(C)
Điều này rất hữu ích khi bạn cần giải quyết các bài toán hình học trong chương trình lớp 11, đặc biệt là trong các bài thi.
Ứng dụng công thức lượng giác trong tam giác lớp 11
Việc nắm vững công thức lượng giác 11 là một yếu tố quan trọng giúp bạn học tốt môn Toán lớp 11. Bài viết này đã cung cấp cho bạn các công thức cơ bản và nâng cao, cũng như ứng dụng chúng vào việc giải quyết các bài toán lượng giác. Chúng tôi hy vọng bài viết này giúp bạn hiểu rõ hơn về lượng giác và áp dụng thành công vào các bài tập. Hãy luyện tập thường xuyên và tham khảo các bài viết khác để nâng cao kiến thức của bạn!