Tính chất hình bình hành
Hình bình hành là một tứ giác có hai cặp cạnh đối song song với nhau. Nói cách khác, trong một hình bình hành, cạnh đối diện vừa song song vừa bằng nhau về độ dài. Hình bình hành còn là một loại tứ giác đặc biệt, trong đó các đường chéo và các góc có những tính chất riêng giúp nhận biết và áp dụng vào các bài toán hình học.
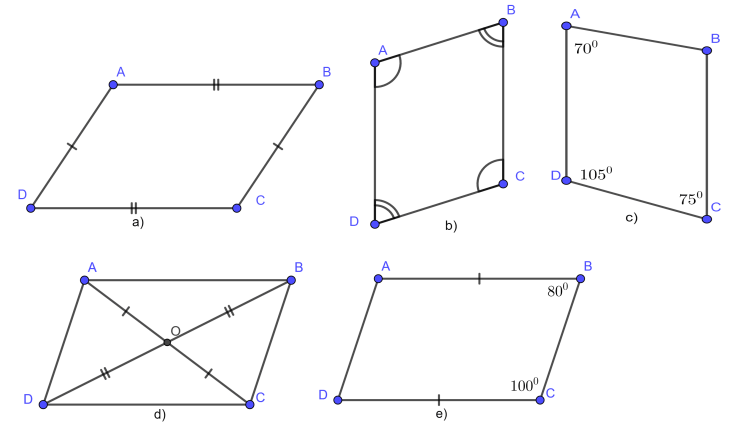
Cách nhận biết hình bình hành:
Qua các cạnh: Nếu một tứ giác có hai cặp cạnh đối song song, đó là hình bình hành.
Qua các góc: Nếu một tứ giác có các góc đối bằng nhau, kết hợp với cạnh đối song song, thì đó là hình bình hành.
Qua các đường chéo: Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường, nghĩa là chia đôi nhau.
Qua tính chất tổng hợp: Một tứ giác có hai cặp cạnh đối bằng nhau và bằng nhau về độ dài, hoặc có đường chéo chia đôi nhau, cũng xác định là hình bình hành.
💡 Mẹo nhận biết nhanh:
Kiểm tra xem các cạnh đối có song song và bằng nhau không.
Kiểm tra đường chéo có cắt nhau tại trung điểm không.
Nếu cả hai điều kiện trên thỏa, chắc chắn tứ giác là hình bình hành.
👉 Nắm rõ khái niệm và cách nhận biết hình bình hành sẽ giúp bạn dễ dàng áp dụng tính chất của hình bình hành để giải các bài toán về diện tích, chu vi, đường chéo hay góc trong hình học.
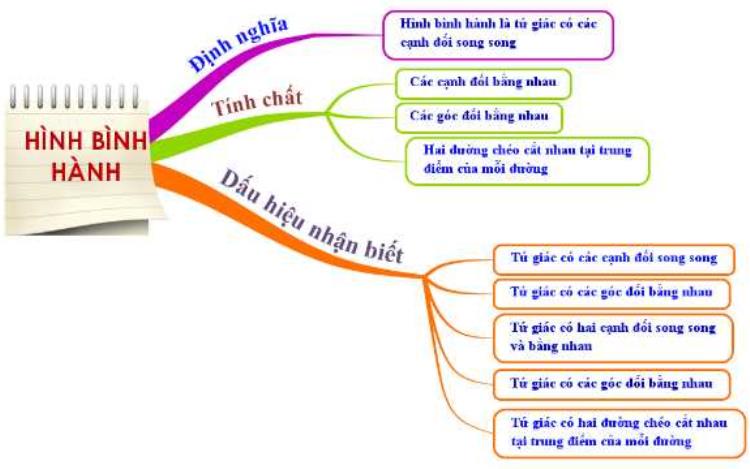
Các tính chất của hình bình hành cơ bản bao gồm những gì?Hình bình hành là một tứ giác đặc biệt, do đó có nhiều tính chất quan trọng mà bạn cần nắm để giải các bài toán hình học hiệu quả. Dưới đây là các tính chất cơ bản của hình bình hành:
Cạnh đối bằng nhau và song song
Hai cặp cạnh đối diện song song với nhau.
Hai cặp cạnh đối bằng nhau về độ dài.
Đây là tính chất quan trọng nhất để nhận biết và chứng minh một tứ giác là hình bình hành.
Góc đối bằng nhau
Các góc đối diện trong hình bình hành bằng nhau.
Tổng hai góc kề nhau bằng 180° , nghĩa là góc kề bù.
Đường chéo
Hai đường chéo cắt nhau tại trung điểm của mỗi đường, nghĩa là chia đôi nhau.
Đường chéo không nhất thiết bằng nhau, nhưng khi cắt nhau tại trung điểm, tạo ra hai cặp tam giác bằng nhau.
Tính chất tổng hợp
Một tứ giác là hình bình hành nếu thỏa mãn một trong các điều kiện sau:
Hai cặp cạnh đối song song.
Hai cặp cạnh đối bằng nhau.
Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Một cặp cạnh đối song song và bằng nhau.
Chu vi và diện tích
Chu vi: Tổng độ dài bốn cạnh, hoặc P=2(a+b) nếu biết hai cạnh kề a và b.
Diện tích: S=a× h, trong đó a là chiều dài đáy và h là chiều cao tương ứng.
💡 Mẹo áp dụng:
Khi gặp bài toán, hãy thử xác định các cặp cạnh đối song song, đường chéo chia đôi để nhận biết hình bình hành.
Sử dụng các tính chất về góc và đường chéo để chứng minh các quan hệ hình học hoặc tính diện tích, chu vi.
👉 Nắm vững các tính chất của hình bình hành này sẽ giúp bạn giải bài tập nhanh chóng, chính xác và áp dụng vào các dạng toán hình học từ cơ bản đến nâng cao.
Hình bình hành là gì và cách nhận biết hình bình hànhDưới đây là công thức tính diện tích và chu vi hình bình hành
Chu vi hình bình hành:
P=2 × (a + b)
Trong đó:
a, b là độ dài hai cạnh kề của hình bình hành.
Diện tích hình bình hành:
S=a × h
Trong đó:
a là độ dài đáy (cạnh đáy).
h là chiều cao tương ứng từ đáy đến cạnh đối diện.
Công thức diện tích theo hai cạnh và góc:
S=a × b × sin(θ)
Trong đó:
a, b là hai cạnh kề.
θ là góc tạo bởi hai cạnh a và b.
💡 Lưu ý:
Dùng công thức thứ nhất (S=a × h) khi biết chiều cao.
Dùng công thức thứ hai (S=a × b × sin(θ)) khi biết hai cạnh và góc giữa chúng.
Để chứng minh một tứ giác là hình bình hành, bạn có thể dựa vào các tính chất cơ bản của hình bình hành. Dưới đây là các cách chứng minh phổ biến:
Dựa vào các cạnh đối song song
Nếu tứ giác có hai cặp cạnh đối song song, thì tứ giác đó là hình bình hành.
Ví dụ: Trong tứ giác ABCD, nếu AB // CD và AD // BC → ABCD là hình bình hành.
Dựa vào các cạnh đối bằng nhau
Nếu tứ giác có hai cặp cạnh đối bằng nhau về độ dài, thì đó là hình bình hành.
Ví dụ: AB=CD và AD=BC → tứ giác ABCD là hình bình hành.
Dựa vào đường chéo
Nếu hai đường chéo cắt nhau tại trung điểm của mỗi đường, tứ giác là hình bình hành.
Ví dụ: Giao điểm O của AC và BD chia đôi AC và BD → ABCD là hình bình hành.
Dựa vào tổng hợp điều kiện
Tứ giác có một cặp cạnh đối song song và bằng nhau, thì đó cũng là hình bình hành.
Đây là trường hợp đặc biệt nhưng cũng giúp chứng minh nhanh.
Sử dụng góc đối bằng nhau
Nếu các góc đối bằng nhau, kết hợp với các cạnh hoặc đường chéo theo các điều kiện trên, tứ giác có thể được xác định là hình bình hành.
💡 Mẹo:
Khi làm bài tập, thường kiểm tra cạnh đối song song hoặc đường chéo chia đôi sẽ nhanh và trực quan nhất.
Sau khi chứng minh tứ giác là hình bình hành, bạn có thể áp dụng các tính chất về diện tích, chu vi, đường chéo, góc để giải tiếp các bài toán khác.

Ứng dụng của hình bình hành trong thực tếCác tính chất của hình bình hành không chỉ quan trọng trong học tập mà còn được ứng dụng rộng rãi trong đời sống và kỹ thuật. Dưới đây là một số ví dụ điển hình:
Thiết kế kiến trúc và xây dựng
Hình bình hành thường xuất hiện trong mặt bằng nhà cửa, nền móng, sân vườn, sàn nhà.
Nhờ tính chất cạnh đối song song và bằng nhau, các kiến trúc sư dễ dàng tính toán diện tích, bố trí các vật dụng hoặc lát gạch sao cho cân đối và thẩm mỹ.
Nội thất và thiết kế đồ dùng
Bàn, ghế, kệ, cửa sổ thường được thiết kế dựa trên hình bình hành để tối ưu không gian và độ cân bằng.
Tính chất góc đối bằng nhau và đường chéo cắt nhau tại trung điểm giúp đảm bảo sự cân đối và ổn định cấu trúc.
Kỹ thuật cơ khí và xây dựng kết cấu
Trong thiết kế cầu, khung nhà thép, giàn giáo, khung hình bình hành giúp phân bố lực đều và giảm nguy cơ bị biến dạng.
Các cấu trúc dạng hình bình hành thường tạo ra sự ổn định và chắc chắn, dễ tính toán lực kéo, lực nén.
Nghệ thuật và trang trí
Hình bình hành được dùng trong hoa văn, gạch lát, họa tiết trang trí, tận dụng tính đối xứng và song song để tạo hình hài hòa.
Tính chất đường chéo chia đôi cũng giúp cân bằng bố cục trong thiết kế.
Toán ứng dụng trong thực tế
Trong kỹ thuật đo đạc, bản đồ, lập kế hoạch khu đất hay sân vườn, tính chất diện tích hình bình hành giúp tính toán nhanh và chính xác.
Ví dụ, khi đo diện tích mảnh đất hình bình hành, chỉ cần biết chiều dài đáy và chiều cao, không cần đo từng góc.
💡 Mẹo:
Khi thiết kế hay tính toán, hãy tận dụng cạnh đối song song, góc đối bằng nhau, đường chéo chia đôi để giảm thiểu sai số và tối ưu hóa không gian.
👉 Như vậy, hiểu và áp dụng tính chất hình bình hành không chỉ giúp giải các bài toán trên lớp mà còn hỗ trợ trong kiến trúc, kỹ thuật, nội thất, trang trí và đo đạc thực tế.
Tóm lại, nắm vững tính chất hình bình hành giúp học sinh và người học nhận biết, chứng minh và giải bài tập hiệu quả. Đồng thời, các tính chất này còn được ứng dụng trong thực tế như kiến trúc, kỹ thuật, trang trí và đo đạc, mang lại sự chính xác và tiện lợi.>> Xem thêm: Xe đi nội bài hưng yên