Công thức lượng giác 11
Lượng giác là môn học nghiên cứu mối quan hệ giữa các góc và các cạnh trong tam giác, đặc biệt là trong tam giác vuông. Trong chương trình lớp 11, các hàm lượng giác cơ bản gồm:
- Sin (sin x): tỉ số giữa cạnh đối và cạnh huyền của góc x trong tam giác vuông.
- Cos (cos x): tỉ số giữa cạnh kề và cạnh huyền của góc x trong tam giác vuông.
- Tan (tan x): tỉ số giữa sin x và cos x, hay cạnh đối/chạy kề.
- Cot (cot x): nghịch đảo của tan x, hay cạnh kề/cạnh đối.
Các hàm lượng giác này được sử dụng để thiết lập các công thức, giúp giải các bài toán về phương trình, tam giác, và các biểu thức phức tạp.

Công thức lượng giác lớp 11 gồm những gì?Công thức lượng giác lớp 11 đầy đủ
Tỉ số lượng giác của một góc nhọn
- Trong một tam giác vuông, với góc nhọn α:
- sin α=cạnh đối / cạnh huyền
- cos α=cạnh kề / cạnh huyền
- tan α=cạnh đối / cạnh kề
- cot α=cạnh kề / cạnh đối
Các công thức lượng giác cơ bản
- sin^2 x+cos^2 x=1
- 1+tan^2 x=1 / cos^2 x
- 1+cot^2 x=1 / sin^2 x
- tan x=sin x / cos x
- cot x=cos x / sin x
Công thức cộng – hiệu
- sin(A + B)=sin A cos B+cos A sin B
- sin(A - B)=sin A cos B - cos A sin B
- cos(A + B)=cos A cos B - sin A sin B
- cos(A - B)=cos A cos B+sin A sin B
- tan(A + B)=(tan A + tan B) / (1 - tan A tan B)
- tan(A - B)=(tan A - tan B) / (1 + tan A tan B)
Công thức nhân lượng giác
Nhân đôi
sin 2A=2 sin A cos A
cos 2A=cos^2 A - sin^2 A=2 cos^2 A - 1=1 - 2 sin^2 A
tan 2A=2 tan A / (1 - tan^2 A)
Nhân ba
sin 3A=3 sin A - 4 sin^3 A
cos 3A=4 cos^3 A - 3 cos A
tan 3A=(3 tan A - tan^3 A) / (1 - 3 tan^2 A)
Nhân bốn
sin 4A=8 sin A cos^3 A - 4 sin^3 A cos A
cos 4A=8 cos^4 A - 8 cos^2 A+1
tan 4A=(4 tan A - 4 tan^3 A) / (1 - 6 tan^2 A + tan^4 A)
Công thức hạ bậc
- sin^2 x=(1 - cos 2x)/2
- cos^2 x=(1 + cos 2x)/2
- sin x cos x=(1/2) sin 2x
Công thức hai góc đặc biệt trên đường tròn
Hai góc đối nhau
cos(-x)=cos x
sin(-x)=-sin x
tan(-x)=-tan x
cot(-x)=-cot x
Hai góc bù nhau
sin(π - x)=sin x
cos(π - x)=-cos x
tan(π - x)=-tan x
cot(π - x)=-cot x
Hai góc phụ nhau
sin(π/2 - x)=cos x
cos(π/2 - x)=sin x
tan(π/2 - x)=cot x
cot(π/2 - x)=tan x
Hai góc hơn hoặc kém π
sin(π + x)=-sin x
cos(π + x)=-cos x
tan(π + x)=tan x
cot(π + x)=cot x
Hai góc hơn hoặc kém π/2
sin(π/2 + x)=cos x
cos(π/2 + x)=-sin x
tan(π/2 + x)=-cot x
cot(π/2 + x)=-tan x
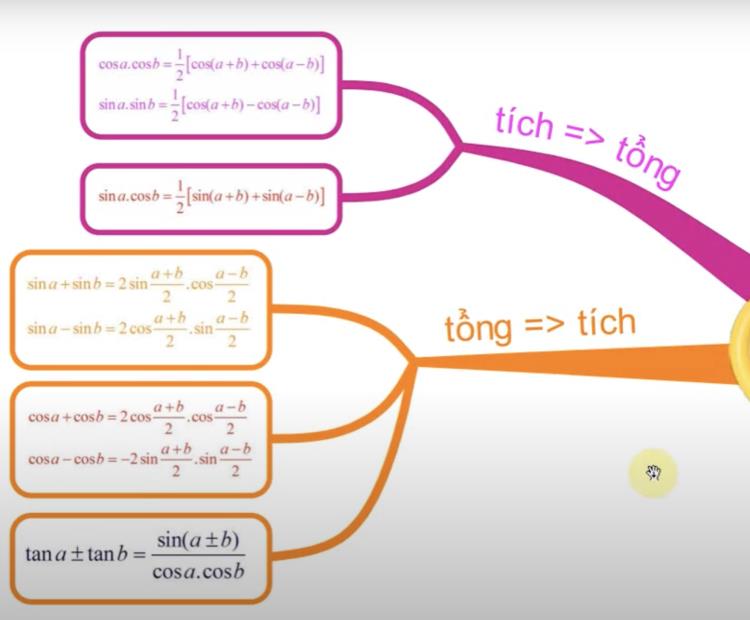
Công thức biến đổi tổng thành tích
- sin A+sin B=2 sin((A + B)/2) cos((A - B)/2)
- sin A - sin B=2 cos((A + B)/2) sin((A - B)/2)
- cos A+cos B=2 cos((A + B)/2) cos((A - B)/2)
- cos A - cos B=-2 sin((A + B)/2) sin((A - B)/2)
Công thức nghiệm phương trình lượng giác cơ bản
- sin a=0 ⇔ a=kπ
- sin a=1 ⇔ a=π/2+k2π
- sin a=-1 ⇔ a=-π/2+k2π
- cos a=0 ⇔ a=π/2+kπ
- cos a=1 ⇔ a=k2π
- cos a=-1 ⇔ a=π+k2π
Làm thế nào để nhớ nhanh công thức lượng giác 11?Để nhớ nhanh công thức lượng giác 11, bạn cần kết hợp hiểu bản chất+mẹo ghi nhớ+luyện tập. Dưới đây là hướng dẫn chi tiết, khoa học mà vẫn dễ áp dụng:
Hiểu bản chất trước khi học thuộc
Không học máy móc, hãy nhớ rằng các công thức lượng giác đều xuất phát từ tam giác vuông và hình tròn lượng giác.
Ví dụ: sin α=đối/huyền → hiểu rằng sin phản ánh “ cạnh đối” so với góc.
Khi bạn hiểu cách hình học liên kết với công thức, trí nhớ sẽ tự nhiên hơn.
Nhóm công thức theo loại
Tỉ số lượng giác cơ bản: sin, cos, tan, cot
Công thức cơ bản: sin² x+cos² x=1, 1+tan² x=1/cos² x…
Công thức tổng – hiệu: sin(A ± B), cos(A ± B), tan(A ± B)
Công thức nhân đôi, nhân ba: sin 2A, cos 2A, tan 2A…
Công thức hạ bậc / biến đổi tổng thành tích
Chia nhỏ giúp não bộ ghi nhớ dễ hơn so với học tất cả cùng một lúc.
Sử dụng “ mẹo âm thanh – câu thơ – từ khóa”
Tỉ số lượng giác tam giác vuông:
“ Sin đi học, Cos không hư, Tan đoàn kết, Cot kết đoàn”
Công thức cộng – hiệu (thơ ngắn):
Cos cộng cos=hai cos cos
Cos trừ cos=trừ hai sin sin
Sin cộng sin=hai sin cos
Sin trừ sin=hai cos sin
Tan tổng=tổng tan / (1 trừ tích tan)
Vẽ sơ đồ hình học
Vẽ tam giác vuông và vòng tròn lượng giác, đánh dấu các cạnh đối, kề, huyền, các góc đặc biệt (0° , 30° , 45° , 60° , 90° ).
Khi nhìn thấy hình → nhớ công thức tự động.
Luyện tập qua bài tập nhỏ
Viết lại công thức nhiều lần → vừa luyện tay vừa nhớ.
Giải nhanh các bài tập dạng tính giá trị lượng giác, chứng minh, biến đổi biểu thức.
Áp dụng ngay vào bài tập → ghi nhớ lâu hơn.
Sử dụng bảng tổng hợp
Tạo bảng 1 trang A4 với:
Bảng giá trị các góc đặc biệt
Công thức cơ bản
Công thức cộng – hiệu
Công thức nhân đôi, nhân ba
Mỗi khi rảnh, xem lại bảng 1-2 phút → bộ nhớ “ ngấm” tự nhiên.
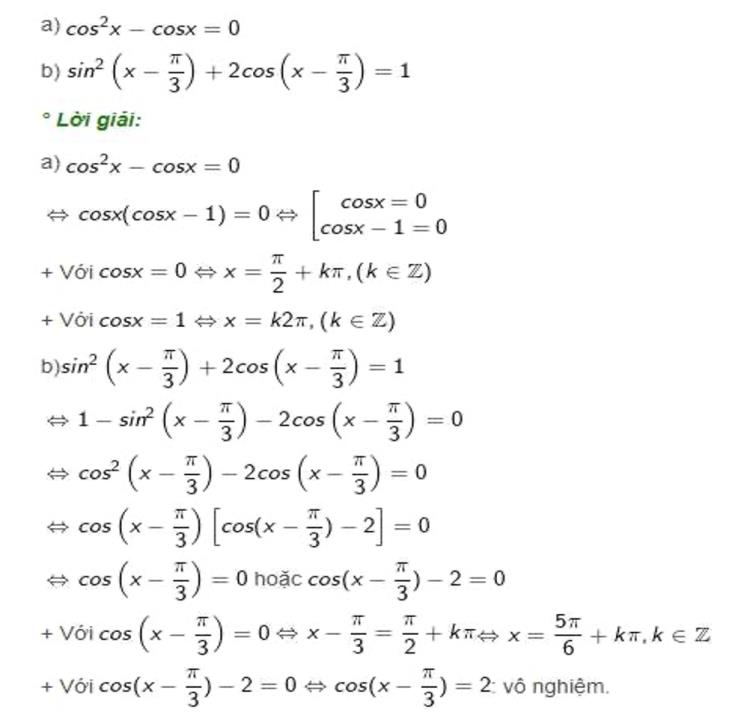
Ví dụ bài tập hay gặp về công thức lượng giác lớp 11Dưới đây là tổng hợp các dạng bài tập hay gặp về công thức lượng giác 11, kèm ví dụ minh họa, được trình bày theo từng nhóm công thức:
Tính giá trị lượng giác của các góc đặc biệt
Dạng bài: Cho góc α (thường là 0° , 30° , 45° , 60° , 90° hoặc π/6, π/4, π/3, π/2), tính sin α, cos α, tan α, cot α.
Ví dụ:
Tính sin 45° , cos 60° , tan 30° , cot 45° .
Lời giải:
sin 45° =√ 2/2
cos 60° =1/2
tan 30° =1/√ 3
cot 45° =1
Sử dụng công thức cơ bản (Pythagore, liên hệ tan-cot)
Dạng bài: Chứng minh các biểu thức lượng giác bằng nhau.
Ví dụ:
Chứng minh: 1+tan² x=1/cos² x
Lời giải:
1+tan² x=1+(sin² x / cos² x)=(cos² x + sin² x)/cos² x=1/cos² x
Công thức cộng – hiệu
Dạng bài: Tính giá trị lượng giác của tổng hoặc hiệu hai góc, hoặc biến đổi biểu thức.
Ví dụ 1: Tính sin(75° )
Lời giải:
sin(75° )=sin(45° + 30° )
=sin45° cos30° +cos45° sin30°
=(√ 2/2)(√ 3/2)+(√ 2/2)(1/2)
=√ 6/4+√ 2/4
=(√ 6 + √ 2)/4
Ví dụ 2: Chứng minh: sin(A + B)+sin(A - B)=2 sin A cos B
Công thức nhân đôi, nhân ba
Dạng bài: Biến đổi biểu thức hoặc tính giá trị lượng giác.
Ví dụ: Tính sin 2x, cos 2x khi sin x=3/5.
Lời giải:
cos x=√ (1 - sin² x)=√ (1 - 9/25)=√ (16/25)=4/5
sin 2x=2 sin x cos x=2*(3/5)*(4/5)=24/25
cos 2x=cos² x - sin² x=(16/25 - 9/25)=7/25
Biến đổi tổng thành tích / tích thành tổng
Dạng bài: Biến đổi biểu thức để giải phương trình hoặc đơn giản hóa.
Ví dụ: Chứng minh: sin A+sin B=2 sin((A + B)/2) cos((A - B)/2)
Lời giải: Áp dụng công thức đã học, thay A, B nếu cần tính giá trị cụ thể.
Phương trình lượng giác cơ bản
Dạng bài: Giải phương trình như sin x=0, cos x=1/2, tan x=√ 3.
Ví dụ: Giải phương trình: sin x=1/2
Lời giải:
sin x=1/2 ⇔ x=π/6+k2π hoặc x=5π/6+k2π (k ∈ Z)
Bài toán ứng dụng hình học
Dạng bài: Tính độ dài, góc trong tam giác sử dụng công thức lượng giác.
Ví dụ: Trong tam giác ABC vuông tại A, AB=3, AC=4. Tính sin B, cos B, tan B.
Lời giải:
BC² =AB² +AC² =3² +4² =25 ⇒ BC=5
sin B=đối/huyền=AC/BC=4/5
cos B=kề/huyền=AB/BC=3/5
tan B=đối/kề=AC/AB=4/3
Trên đây, chúng tôi đã chia sẻ chi tiết về công thức lượng giác 11, từ tỉ số lượng giác cơ bản, công thức cộng – hiệu, nhân đôi, hạ bậc, đến các công thức biến đổi tổng – tích và phương trình lượng giác. Hy vọng bài viết này sẽ giúp bạn nắm vững kiến thức và ghi nhớ nhanh chóng các công thức quan trọng, hỗ trợ hiệu quả trong học tập và giải toán.
Nếu bạn đang cần dịch vụ cho thuê xe, xe đi đường dài, xe đi tour du lịch Hà Nội hoặc xe đưa đón sân golf, hãy liên hệ ngay với XE NỘI BÀI 3T – đơn vị vận tải uy tín với đội ngũ tài xế chuyên nghiệp và chất lượng dịch vụ hàng đầu.
📞 Hotline tư vấn miễn phí: 0941.057.750