Công thức lượng giác 11
Nói đến chương trình Toán lớp 11, lượng giác chắc chắn là phần kiến thức khiến nhiều học sinh e ngại. Nguyên nhân chính không nằm ở việc công thức quá khó, mà do bạn chưa biết cách hệ thống chúng một cách rõ ràng, dễ hiểu. Thực tế, công thức lượng giác 11 không hề rối rắm nếu bạn biết nhóm lại theo từng mục đích sử dụng, thay vì học lan man từng công thức một cách rời rạc.
Học lượng giác lớp 11 không chỉ giúp bạn giải bài tập dễ dàng hơn mà còn là nền tảng cực kỳ quan trọng khi học đạo hàm, tích phân hoặc giải các bài toán phức tạp hơn sau này. Do đó, việc nắm chắc các công thức ngay từ bây giờ là điều vô cùng cần thiết để bạn không bị hổng kiến thức.
Đừng học vẹt, hãy học theo nhóm công thức
Để dễ nhớ hơn, thay vì cố gắng nhồi nhét từng công thức riêng lẻ, bạn nên học theo từng nhóm nhỏ như nhóm cơ bản, nhóm cộng trừ, nhóm nhân đôi, nhóm hạ bậc… Việc phân nhóm giúp não bộ dễ ghi nhớ và biết cách vận dụng linh hoạt hơn khi làm bài.
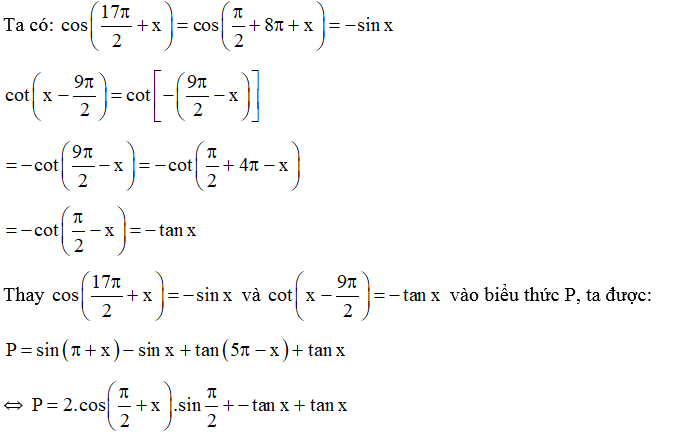
Bảng hệ thống công thức lượng giác lớp 11 đầy đủ, dễ hiểuCông thức lượng giác lớp 11 rất đa dạng nhưng không hề khó nếu bạn biết cách sắp xếp khoa học. Dưới đây là cách hệ thống lại theo từng nhóm, giúp bạn học nhanh hơn.
Công thức cơ bản của lượng giác
Công thức cơ bản chính là nền móng giúp bạn dễ dàng nhận diện và biến đổi các bài toán. Những công thức này thường xuyên lặp lại trong mọi dạng bài nên bạn cần ghi nhớ kỹ.
sin^2x+cos^2x=1
1+tan^2x=1 / cos^2x
1+cot^2x=1 / sin^2x
Ba công thức trên tưởng đơn giản nhưng lại là “ xương sống” để bạn giải hầu hết các bài tập liên quan đến lượng giác.
Công thức cộng trừ và nhân đôi giúp biến đổi dễ dàng
Khi gặp các bài toán liên quan đến góc tổng, góc hiệu, công thức cộng trừ chính là công cụ giúp bạn tháo gỡ nhanh chóng.
sin(a ± b)=sin a cos b ± cos a sin b
cos(a ± b)=cos a cos b ∓ sin a sin b
tan(a ± b)=(tan a ± tan b) / (1 ∓ tan a tan b)
Bên cạnh đó, công thức nhân đôi giúp rút gọn hoặc biến đổi nhanh những biểu thức có dạng 2x.
sin 2a=2 sin a cos a
cos 2a=cos^2a - sin^2a=2 cos^2a - 1=1 - 2 sin^2a
tan 2a=2 tan a / (1 - tan^2a)
Nhìn qua có vẻ nhiều nhưng thực tế chúng đều tuân theo quy luật rất dễ nhận biết nếu bạn luyện tập thường xuyên.
Công thức hạ bậc và biến đổi tích thành tổng
Khi giải các bài toán liên quan đến đạo hàm, tích phân, công thức hạ bậc sẽ giúp bạn biến đổi những lũy thừa sin, cos về dạng đơn giản hơn để dễ xử lý.
sin^2a=(1 - cos 2a) / 2
cos^2a=(1 + cos 2a) / 2
Đừng quên nhóm công thức biến đổi tích thành tổng, bởi nó sẽ giúp bạn “ gỡ rối” những biểu thức tưởng chừng rất khó chịu:
sin a sin b=1/2 [cos(a - b) - cos(a + b)]
cos a cos b=1/2 [cos(a - b)+cos(a + b)]
sin a cos b=1/2 [sin(a + b)+sin(a - b)]
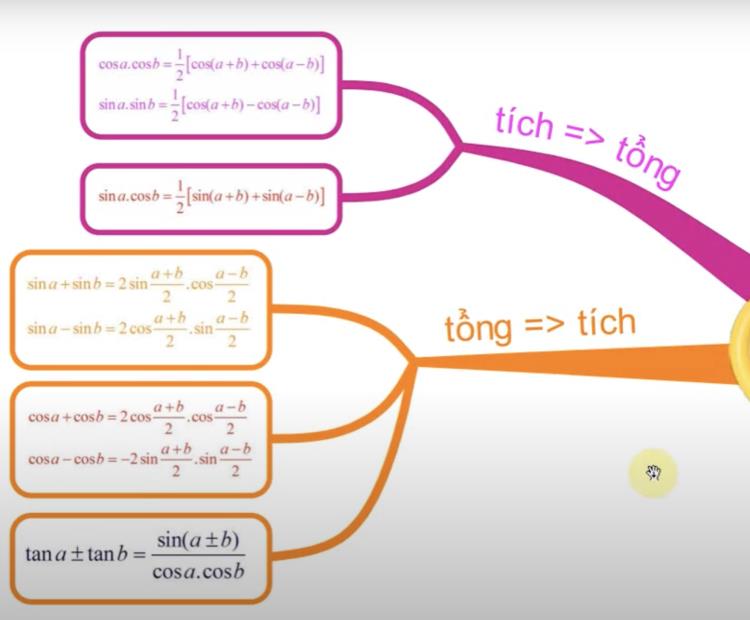
Học sinh ôn tập công thức lượng giác lớp 11 với sơ đồ tư duyRất nhiều học sinh cảm thấy các công thức lượng giác giống nhau, dễ nhầm dấu cộng, dấu trừ. Để khắc phục điều này, bạn cần luyện thói quen viết lại công thức mỗi khi giải bài, từ đó ghi nhớ tự nhiên hơn thay vì học thuộc lòng khô khan.
Mẹo ghi nhớ công thức lượng giác theo quy luật
Một mẹo nhỏ giúp bạn dễ nhớ chính là hãy để ý quy luật giữa các công thức. Ví dụ, công thức cộng trừ sin cos luôn đi cặp dấu cộng trừ. Khi sin a ± b thì bên phải công thức cũng ± theo. Còn với cos a ± b thì bên phải lại đảo dấu ∓.
Với công thức nhân đôi, bạn chỉ cần nhớ công thức sin 2a=2 sin a cos a trước, các công thức còn lại về cos, tan đều có thể suy ra từ đó. Việc ghi nhớ theo kiểu mắt xích này sẽ giúp bạn tự động liên kết các công thức với nhau khi cần áp dụng.
Áp dụng nhiều dạng bài tập để ghi nhớ tự nhiên
Chỉ khi làm bài tập thường xuyên, bạn mới thật sự hiểu và nhớ lâu công thức lượng giác lớp 11. Hãy thử áp dụng vào các bài tập từ cơ bản đến nâng cao, mỗi lần sai hãy rà lại nguyên nhân sai công thức hay sai biến đổi để không lặp lại lỗi.

Áp dụng công thức lượng giác vào bài tập lớp 11Công thức lượng giác không chỉ dừng lại trong khuôn khổ bài tập lớp 11. Chúng còn xuất hiện liên tục trong các bài thi tốt nghiệp, đại học hay các dạng toán hình học, phương trình phức tạp ở những cấp độ cao hơn.
Khi nào cần áp dụng công thức lượng giác?
Nếu bài yêu cầu biến đổi biểu thức lượng giác về dạng đơn giản hoặc cần giải phương trình, bạn sẽ bắt buộc phải sử dụng các công thức cơ bản, cộng trừ, nhân đôi, hạ bậc. Các bài tích phân, đạo hàm cũng không thể thiếu sự hỗ trợ của nhóm công thức này.
Trong thực tế, lượng giác còn được ứng dụng nhiều trong xây dựng, thiết kế, lập trình, thậm chí là nghiên cứu vật lý, thiên văn học. Các công thức sin, cos giúp đo đạc, tính toán chính xác các đại lượng liên quan đến góc, độ dài, chu kỳ…
Luyện thói quen sử dụng lượng giác như công cụ hỗ trợ tư duy
Càng luyện tập nhiều, bạn sẽ càng nhận ra rằng lượng giác không khó như tưởng tượng. Hãy coi công thức lượng giác như một “ người bạn thân” hỗ trợ bạn giải quyết những bài toán khó nhằn một cách logic, hệ thống.
Công thức lượng giác 11 là phần không thể thiếu trong hành trình chinh phục môn Toán. Khi đã nắm chắc, bạn sẽ thấy lượng giác không còn khó hay khô khan như trước. Quan trọng nhất là xây dựng thói quen luyện tập đều đặn, học theo nhóm công thức rõ ràng, từ đó vận dụng dễ dàng, làm bài chính xác và đạt kết quả tốt.