Công thức lượng giác 11
Lượng giác là một phần quan trọng trong chương trình Toán lớp 11 và cũng là kiến thức nền tảng cho nhiều chuyên đề khác trong Toán học sau này. Khi học về công thức lượng giác 11, bạn sẽ bắt gặp rất nhiều dạng công thức khác nhau như công thức cơ bản, công thức cộng, nhân đôi, hạ bậc, biến đổi tích thành tổng… Dù đa dạng, nhưng nếu nắm được bản chất, bạn sẽ thấy việc học không hề khó.
Hiểu rõ các công thức lượng giác 11 không chỉ giúp bạn giải quyết nhanh gọn các bài tập trong sách giáo khoa hay đề thi, mà còn rèn luyện khả năng tư duy logic, khả năng biến đổi linh hoạt các biểu thức Toán học. Nhờ đó, bạn sẽ dần hình thành phản xạ tốt khi gặp các dạng toán lượng giác trong đề kiểm tra hay các kỳ thi lớn.
Trong thực tế, lượng giác còn được ứng dụng rộng rãi trong kỹ thuật, công nghệ, kiến trúc, cơ khí… Việc ghi nhớ công thức lượng giác lớp 11 từ sớm sẽ là hành trang vững chắc cho những ai có định hướng theo đuổi các ngành học liên quan.
Tầm Quan Trọng Của Việc Học Thuộc Công Thức Lượng Giác
Việc học thuộc công thức lượng giác lớp 11 giống như việc bạn trang bị " vũ khí" để chiến đấu với các bài toán khó. Khi đã thuộc lòng, bạn không mất thời gian tra cứu hay dò lại từng bước, từ đó nâng cao tốc độ làm bài, đặc biệt trong các kỳ thi quan trọng.

Bảng công thức lượng giác lớp 11 cơ bảnĐể dễ nhớ, bạn nên hệ thống công thức lượng giác lớp 11 thành từng nhóm theo tính chất. Dưới đây là các công thức cơ bản và thường xuyên được sử dụng nhất.
Công thức lượng giác cơ bản:
sin^2x+cos^2x=1
1+tan^2x=1 / cos^2x
1+cot^2x=1 / sin^2x
Công thức cộng:
sin(a ± b)=sin a cos b ± cos a sin b
cos(a ± b)=cos a cos b ∓ sin a sin b
tan(a ± b)=(tan a ± tan b) / (1 ∓ tan a tan b)
Công thức nhân đôi:
sin 2a=2 sin a cos a
cos 2a=cos^2a - sin^2a=2 cos^2a - 1=1 - 2 sin^2a
tan 2a=2 tan a / (1 - tan^2a)
Công thức hạ bậc:
sin^2a=(1 - cos 2a) / 2
cos^2a=(1 + cos 2a) / 2
Công thức biến đổi tích thành tổng:
sin a sin b=1/2 [cos(a - b) - cos(a + b)]
cos a cos b=1/2 [cos(a - b)+cos(a + b)]
sin a cos b=1/2 [sin(a + b)+sin(a - b)]
Việc ghi nhớ các công thức lượng giác lớp 11 theo từng nhóm như trên sẽ giúp bạn dễ hệ thống kiến thức, từ đó làm bài chính xác hơn, không bị nhầm lẫn.
Học Công Thức Theo Cách Nhẹ Nhàng Hơn
Chúng tôi khuyên bạn nên kết hợp việc học thuộc với vẽ sơ đồ tư duy hoặc ghi chú theo sơ đồ hình cây, chia nhóm rõ ràng. Điều này giúp bạn dễ nhớ hơn thay vì học thuộc lòng máy móc.
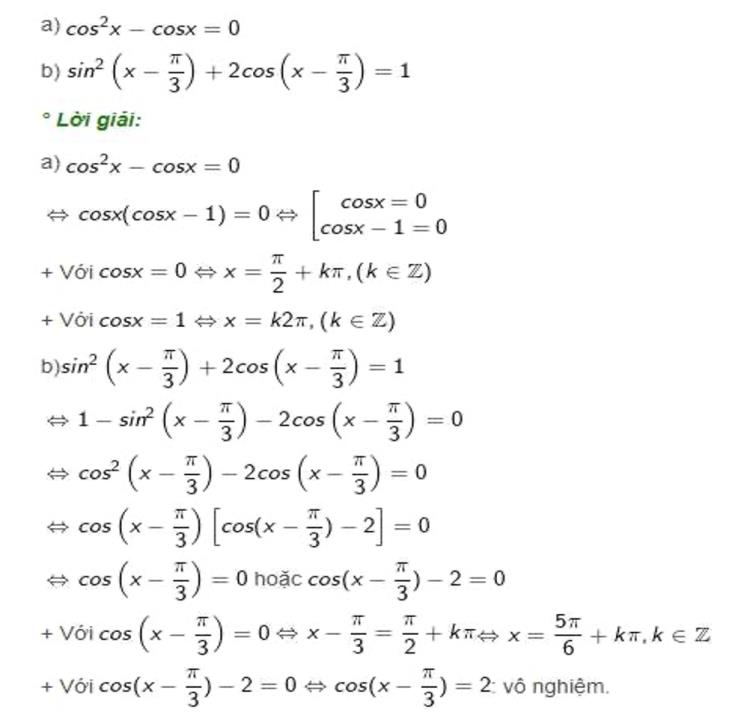
Ví dụ minh họa các dạng bài tập lượng giác lớp 11Nhiều bạn cho rằng công thức lượng giác lớp 11 khó học thuộc bởi chúng rời rạc và quá nhiều biến thể. Thực tế, chỉ cần có phương pháp phù hợp, bạn hoàn toàn có thể ghi nhớ dễ dàng và áp dụng chính xác.
Bí quyết đầu tiên chính là học theo nhóm công thức. Như đã nêu, lượng giác 11 được chia thành các nhóm chính, nếu học theo từng nhóm, bạn sẽ nhớ lâu hơn và không bị nhầm lẫn. Ví dụ, khi nhắc tới " công thức cộng" , bạn sẽ liên kết luôn đến các công thức sin, cos, tan có dạng a ± b.
Thứ hai, hãy liên tục luyện bài tập thực hành. Việc áp dụng công thức vào thực tế sẽ giúp bạn hiểu sâu, nhớ kỹ hơn thay vì chỉ học vẹt. Khi giải nhiều dạng bài khác nhau, bạn sẽ biết nên sử dụng công thức nào trong từng tình huống cụ thể.
Cuối cùng, đừng quên kết hợp ghi chú bằng màu sắc, sơ đồ hình ảnh để bộ não ghi nhớ tốt hơn. Những phương pháp học trực quan này luôn mang lại hiệu quả cao hơn so với cách học truyền thống.
Tránh Sai Lầm Khi Học Lượng Giác
Rất nhiều bạn thường nhầm lẫn giữa các dấu cộng, trừ trong công thức hoặc sai vị trí của sin, cos. Vì thế, việc viết đi viết lại nhiều lần công thức sẽ giúp bạn quen tay, hạn chế tối đa lỗi sai cơ bản này khi làm bài thi.
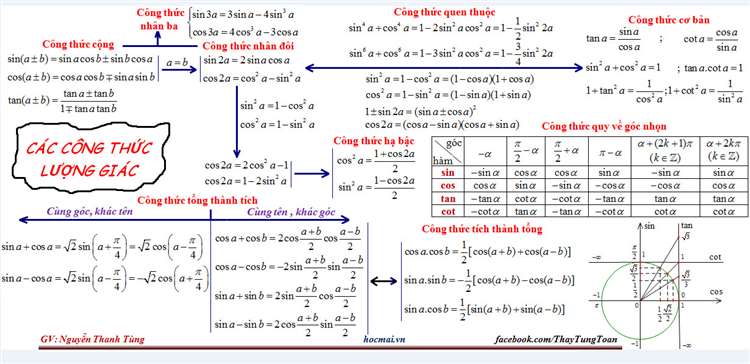
Sơ đồ hệ thống công thức lượng giác lớp 11 dễ nhớKhi nắm vững công thức lượng giác lớp 11, bạn sẽ nhận thấy Toán học trở nên dễ thở hơn rất nhiều. Không còn cảnh loay hoay không biết bắt đầu từ đâu, bạn sẽ chủ động nhận biết dạng bài, xác định công thức phù hợp ngay khi đọc đề.
Trong chương trình lớp 11, các bài tập về lượng giác không đơn thuần chỉ yêu cầu bạn áp dụng một công thức, mà còn đòi hỏi khả năng kết hợp nhiều công thức với nhau để biến đổi biểu thức phức tạp về dạng đơn giản hơn. Chính vì vậy, hiểu sâu, nhớ kỹ các công thức cơ bản sẽ giúp bạn dễ dàng " gỡ rối" những bài toán khó.
Ngoài học tập, lượng giác còn ứng dụng thực tế trong đời sống và các ngành nghề kỹ thuật. Ví dụ, trong xây dựng, lượng giác giúp tính toán góc nghiêng, độ dài, chiều cao của công trình. Trong công nghệ, lượng giác tham gia vào lập trình đồ họa, xử lý hình ảnh, âm thanh…
Khi Nào Cần Ứng Dụng Công Thức Lượng Giác?
Ngoài các bài toán hình học, phương trình lượng giác, bạn còn cần sử dụng công thức lượng giác khi học về đạo hàm, tích phân, tổ hợp xác suất, hình học không gian… Việc thành thạo lượng giác giúp bạn dễ dàng học tiếp các phần kiến thức nâng cao ở lớp 12 và đại học.
Công thức lượng giác 11 là hành trang không thể thiếu với bất kỳ học sinh nào theo đuổi khối tự nhiên. Khi đã nắm chắc, bạn sẽ thấy việc học Toán trở nên nhẹ nhàng và thú vị hơn rất nhiều. Đừng quên luyện tập thường xuyên, hệ thống lại kiến thức qua sơ đồ tư duy để ghi nhớ lâu hơn, chính xác hơn.