Nhị thức Newton
Khi nhắc đến công thức Newton, nhiều người sẽ lập tức nhớ về những bài học đại số trong chương trình trung học. Thực chất, công thức Newton chính là một công cụ toán học vô cùng quan trọng, giúp bạn khai triển biểu thức lũy thừa của tổng hai số hạng. Nói một cách dễ hiểu, công thức này giúp biểu diễn (a + b)^n dưới dạng tổng nhiều hạng tử cụ thể, thay vì nhân tay liên tục.
Nhị thức Newton được nhà toán học nổi tiếng Isaac Newton phát triển vào thế kỷ XVII. Dù cho ra đời từ rất lâu, nhưng đến ngày nay, công thức này vẫn đóng vai trò quan trọng trong nhiều lĩnh vực, từ toán học cơ bản, vật lý đến xác suất thống kê.
Công thức tổng quát của công thức Newton như sau:
(a + b)^n=C(n, 0)a^n+C(n, 1)a^(n-1)b+C(n, 2)a^(n-2)b^2+...+C(n, n)b^n
Trong đó:
C(n, k)=n ! / (k !(n-k) !)
Với công thức này, bạn dễ dàng khai triển bất kỳ biểu thức nào dạng (a + b)^n thành một tổng gồm các hạng tử riêng lẻ, mỗi hạng tử đều có hệ số xác định bởi tổ hợp C(n, k).
Chúng tôi tin rằng, hiểu đúng công thức Newton ngay từ đầu sẽ giúp bạn học toán nhẹ nhàng và hiệu quả hơn rất nhiều.
Nhị Thức Newton Có Ý Nghĩa Gì Trong Học Tập?
Công thức Newton không chỉ là công cụ giải bài tập, nó còn giúp bạn rèn luyện khả năng tư duy logic và tiếp cận toán học theo hướng quy luật. Khi hiểu được bản chất khai triển này, bạn sẽ thấy những công thức khô khan trở nên dễ nhớ và có hệ thống hơn.
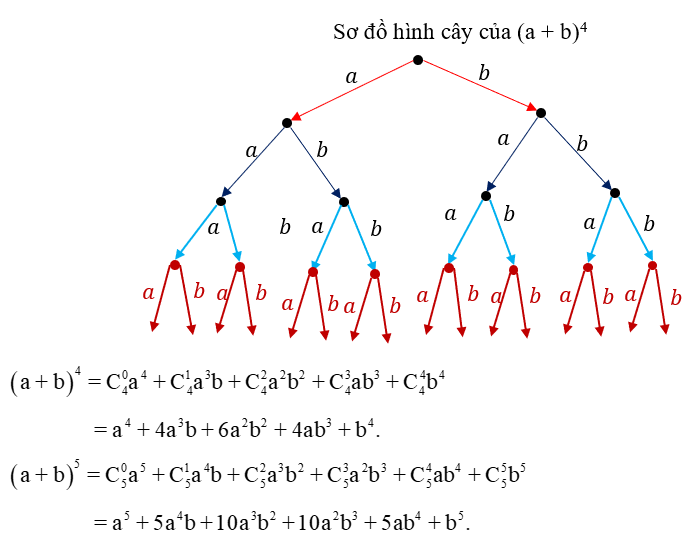
Sơ đồ minh họa công thức công thức Newton cơ bảnBạn có biết rằng công thức Newton không phải là một phát minh hoàn toàn mới của Isaac Newton? Thực chất, người Trung Quốc từ thời cổ đại đã biết đến dạng công thức khai triển này. Tuy nhiên, phải đến khi Newton hệ thống hóa và chứng minh một cách đầy đủ, công thức này mới chính thức được công nhận rộng rãi trong nền toán học hiện đại.
Việc Newton công bố công trình về nhị thức không chỉ giúp ông khẳng định tên tuổi mà còn tạo tiền đề cho hàng loạt phát minh toán học về sau. Nhờ công thức Newton, các nhà khoa học có thêm công cụ để tiếp cận các bài toán phức tạp hơn về giải tích, chuỗi số, cũng như trong việc giải các phương trình đại số cao cấp.
Trong lịch sử, nhiều nhà toán học châu Âu cũng đóng góp vào quá trình hoàn thiện và mở rộng ý nghĩa của công thức Newton, chẳng hạn như Blaise Pascal với tam giác Pascal nổi tiếng, vốn chính là bảng giá trị của các hệ số C(n, k) trong công thức khai triển.
Ứng Dụng Lịch Sử Của Nhị Thức Newton
Ngoài việc giúp học sinh học tốt toán hơn, công thức Newton còn có ảnh hưởng lớn đến các ngành khoa học. Trong vật lý, công thức này hỗ trợ mô hình hóa các hiện tượng có tính chu kỳ hoặc biến thiên. Trong xác suất thống kê, nó được dùng để phân tích tổ hợp, hoán vị, xác suất biến cố.

Ví dụ minh họa khai triển công thức NewtonTrong thực tế học tập, công thức Newton thường được vận dụng để khai triển những biểu thức có số mũ lớn một cách nhanh chóng, chính xác. Thay vì nhân thủ công từng bước, bạn chỉ cần áp dụng công thức một cách hệ thống.
Ví dụ cụ thể:
Khai triển (x + 2)^3.
Theo công thức Newton, ta có:
(x + 2)^3=C(3, 0)x^3+C(3, 1)x^22+C(3, 2)x2^2+C(3, 3)2^3
=1x^3+3x^22+3x4+1*8
=x^3+6x^2+12x+8
Bạn có thể thấy, chỉ cần nắm vững công thức, việc khai triển trở nên vô cùng dễ dàng. Đây chính là lý do công thức Newton luôn xuất hiện trong các đề thi từ cấp 2 đến đại học.
Một mẹo nhỏ để bạn học tốt hơn chính là luyện viết thật nhiều dạng khai triển tương tự, giúp ghi nhớ hệ số tổ hợp nhanh hơn và rèn luyện sự chính xác trong phép tính.
Những Sai Lầm Khi Áp Dụng Nhị Thức Newton
Rất nhiều bạn học sinh nhầm lẫn khi quên mất hệ số tổ hợp hoặc nhầm vị trí số mũ giữa a và b. Để hạn chế sai sót, chúng tôi khuyên bạn nên viết sẵn cấu trúc mẫu cho từng bài, sau đó điền số cụ thể vào. Việc luyện tập nhiều lần cũng giúp bạn làm quen với dạng toán này nhanh chóng hơn.
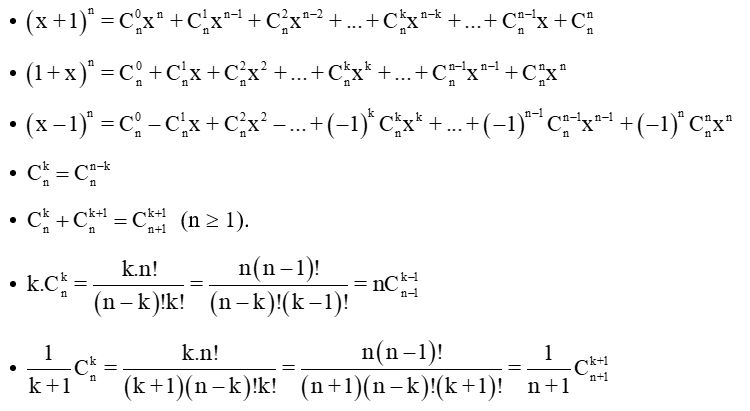
Ứng dụng công thức NewtonCó thể bạn chưa nhận ra, công thức Newton không chỉ dừng lại ở sách vở hay bài kiểm tra. Trên thực tế, công thức này có mặt trong rất nhiều lĩnh vực từ kỹ thuật, công nghệ cho tới tài chính.
Trong lập trình máy tính, công thức Newton hỗ trợ tính toán thuật toán liên quan đến tổ hợp, xác suất, chuỗi nhị phân. Nhờ vậy, các hệ thống AI, machine learning có thể xử lý dữ liệu hiệu quả hơn.
Trong lĩnh vực tài chính, mô hình lãi suất kép hoặc dự báo tài chính theo chuỗi biến động cũng vận dụng nguyên lý của công thức Newton để dự đoán biến số.
Với kỹ thuật xây dựng, kiến trúc, công thức Newton giúp phân tích độ bền, khả năng chịu lực của vật liệu qua từng lớp cấu trúc khác nhau, từ đó đưa ra các mô hình chịu tải phù hợp.
Công Thức Newton Trong Đời Sống Hằng Ngày
Ngay cả khi bạn không làm việc trong các ngành kể trên, công thức Newton vẫn có thể giúp ích cho tư duy logic, đặc biệt khi bạn cần lập kế hoạch hoặc phân tích một vấn đề phức tạp thành nhiều phần nhỏ để giải quyết từng bước.
Nhị thức Newton không chỉ là một công cụ học toán, nó còn giúp bạn phát triển tư duy, rèn luyện sự logic và hệ thống hóa vấn đề. Khi đã nắm vững bản chất và cách vận dụng, bạn sẽ thấy việc học toán trở nên thú vị hơn. Đừng ngần ngại áp dụng công thức Newton vào các bài toán thực tế để hiểu sâu và nhớ lâu hơn nhé.